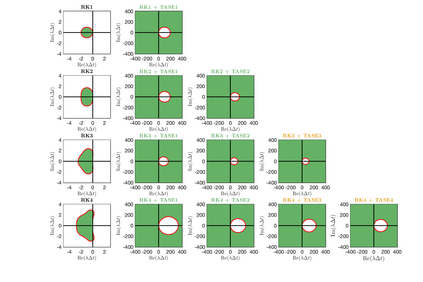
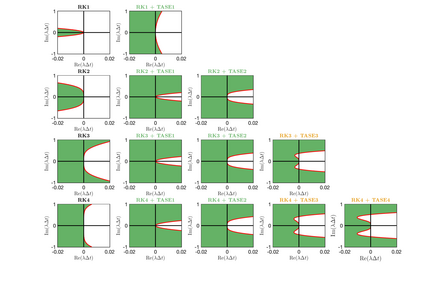
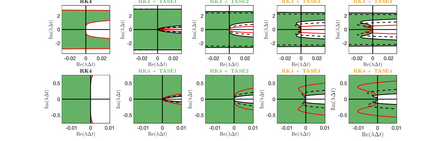
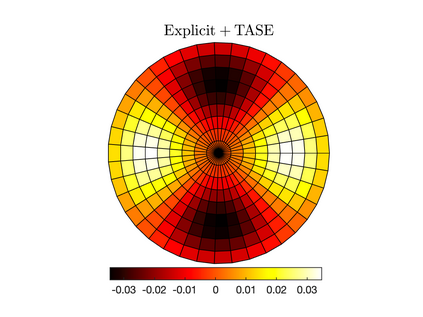
Unconditionally stable implicit time-marching methods are powerful in solving stiff differential equations efficiently. In this work, a novel framework to handle stiff physical terms implicitly is proposed. Both physical and numerical stiffness originating from convection, diffusion and source terms (typically related to reaction) can be handled by a set of predefined Time-Accurate and highly-Stable Explicit (TASE) operators in a unified framework. The proposed TASE operators act as preconditioners on the stiff terms and can be deployed to any existing explicit time-marching methods straightforwardly. The resulting time integration methods remain the original explicit time-marching schemes, yet with nearly unconditional stability. The TASE operators can be designed to be arbitrarily high-order accurate with Richardson extrapolation such that the accuracy order of original explicit time-marching method is preserved. Theoretical analyses and stability diagrams show that the $s$-stages $s$th-order explicit Runge-Kutta (RK) methods are unconditionally stable when preconditioned by the TASE operators with order $p \leq s$ and $p \leq 2$. On the other hand, the $s$th-order RK methods preconditioned by the TASE operators with order of $p \leq s$ and $p > 2$ are nearly unconditionally stable. The only free parameter in TASE operators can be determined a priori based on stability arguments. Unlike classical implicit methods, the TASE methodology allows for solving non-linear problems with arbitrary order without requiring solving a nonlinear system of equations. A set of benchmark problems with strong stiffness is simulated to assess the performance of the TASE method. Numerical results suggest that the proposed framework preserves the high-order accuracy of the explicit time-marching methods with very-large time steps for all the considered cases.
翻译:无条件稳定的隐含时间总体方法在有效解决严格差异方程式方面非常有力。 在这项工作中, 隐含地提议了一个处理严格物理术语的新框架。 源于对流、 扩散和源术语( 通常与反应相关) 的物理和数字僵硬性, 可以由一组预先定义的时间- 准确性和高度稳定( TASE) 操作员在一个统一的框架内处理。 拟议的 TASE 操作员以苛刻的条件作为先决条件, 并可以直接地部署到任何现有的明确时间总体方法中。 由此产生的时间整合方法仍然是最初的清晰时间总体计划, 但却几乎是无条件的。 TASE 操作员可以被设计为任意的高度命令、 扩散和源( 通常与反应相关) 。 理论分析和稳定性图表显示, 美元阶段- 直线 运行- kutta (RK) 方法只有在TASE 操作员以美元为先决条件的情况下, 直线 和 美元 直线 直线 直线 直线 和 美元 直线 直线 直线 直线 直径 直径 直径 直径 直径 直径 直径 直径 直径 直径 直径 的操作器 。 运行 运行 运行 运行 操作者 操作者 的运行者 的运行者 的运行者 的运行者 以 快速 直径 快速 快速 平 平 平 平 方法 。 。