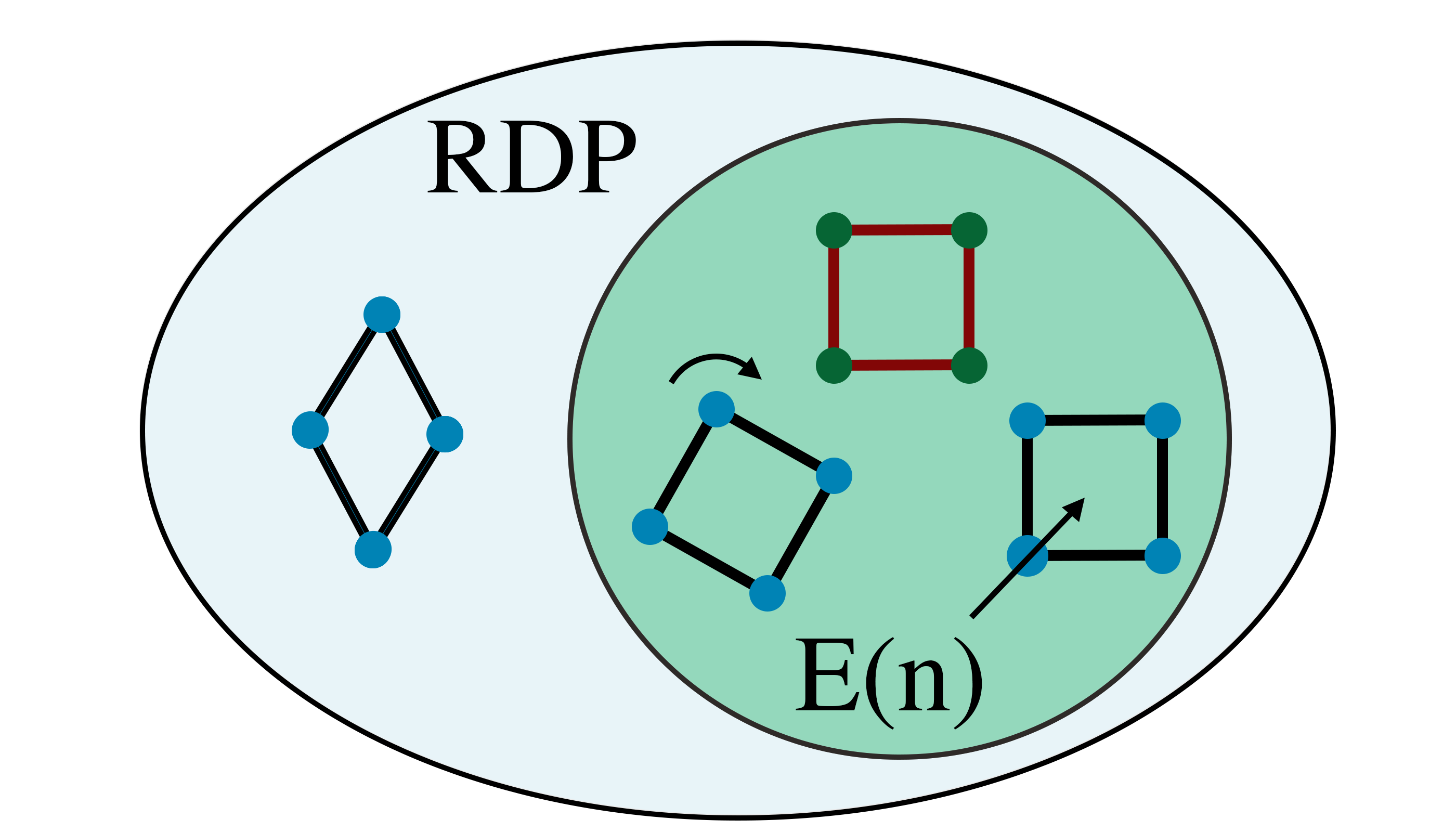
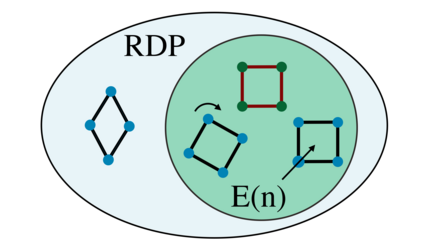
We introduce a novel architecture for graph networks which is equivariant to any transformation in the coordinate embeddings that preserves the distance between neighbouring nodes. In particular, it is equivariant to the Euclidean and conformal orthogonal groups in $n$-dimensions. Thanks to its equivariance properties, the proposed model is extremely more data efficient with respect to classical graph architectures and also intrinsically equipped with a better inductive bias. We show that, learning on a minimal amount of data, the architecture we propose can perfectly generalise to unseen data in a synthetic problem, while much more training data are required from a standard model to reach comparable performance.
翻译:我们引入了一个用于图形网络的新结构,这个结构对于协调嵌入的任何转换都具有等同性,从而保持相邻节点之间的距离。 特别是,它对于以美元为单位的欧clidean和正统正方形组来说具有等同性。 由于其等同性属性,拟议的模型在古典图形结构方面极具数据效率,而且本身也具备更好的感化偏差。 我们表明,我们提出的结构在学习少量数据后,可以完全概括合成问题中的不可见数据,同时需要从标准模型获得更多的培训数据才能达到可比的性能。