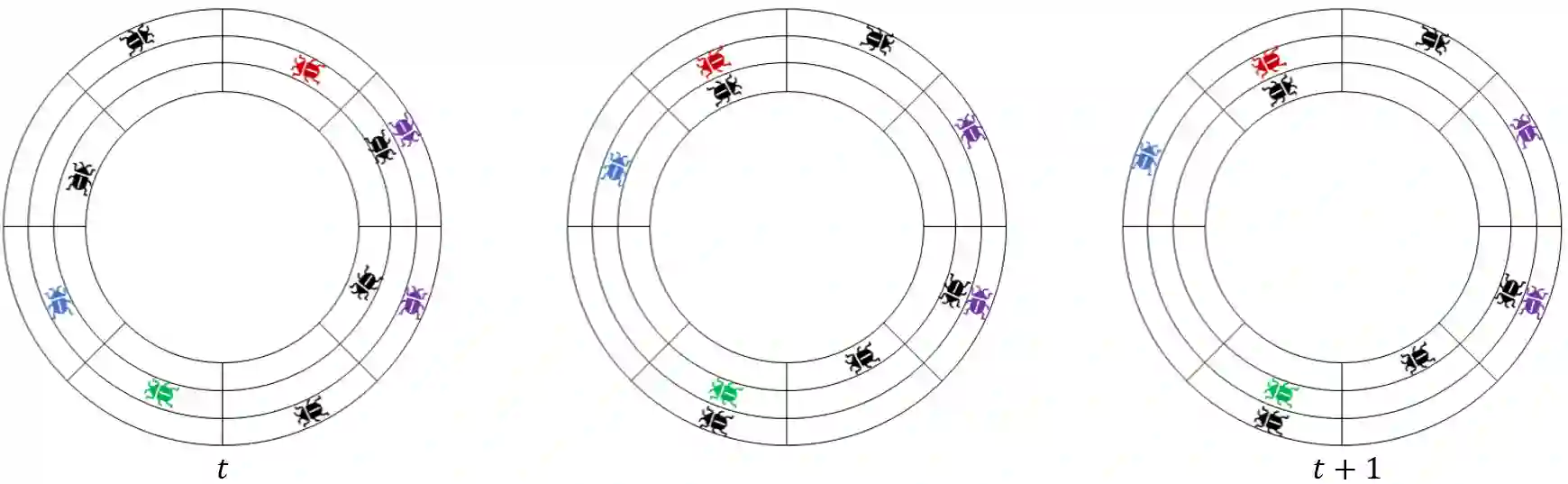
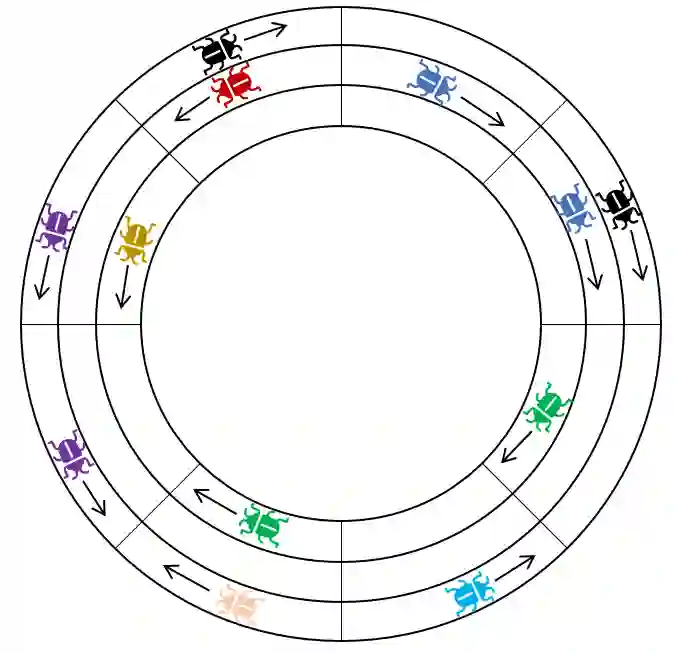
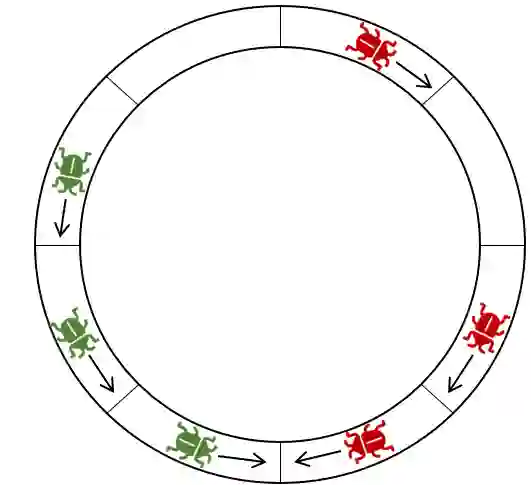
We study the collective motion of autonomous mobile agents on a ringlike environment. The agents' dynamics is inspired by known laboratory experiments on the dynamics of locust swarms. In these experiments, locusts placed at arbitrary locations and initial orientations on a ring-shaped arena are observed to eventually all march in the same direction. In this work we ask whether, and how fast, a similar phenomenon occurs in a stochastic swarm of simple agents whose goal is to maintain the same direction of motion for as long as possible. The agents are randomly initiated as marching either clockwise or counterclockwise on a wide ring-shaped region, which we model as $k$ "narrow" concentric tracks on a cylinder. Collisions cause agents to change their direction of motion. To avoid this, agents may decide to switch tracks so as to merge with platoons of agents marching in their direction. We prove that such agents must eventually converge to a local consensus about their direction of motion, meaning that all agents on each narrow track must eventually march in the same direction. We give asymptotic bounds for the expected amount of time it takes for such convergence or "stabilization" to occur, which depends on the number of agents, the length of the tracks, and the number of tracks. We show that when agents also have a small probability of "erratic", random track-jumping behaviour, a global consensus on the direction of motion across all tracks will eventually be reached. Finally, we verify our theoretical findings in numerical simulations.
翻译:我们在环状环境中研究自主移动物剂的集体运动。 代理人的动力来自关于蝗虫群动态的已知实验室实验。 在这些实验中, 在任意地点放置的蝗虫和环形舞台上的初始方向被观察到最终所有向同一方向进军。 在这项工作中, 我们问, 类似现象是否以及多快地发生在一个简单物剂群中, 这些物剂的目标是尽可能长久地保持同样的运动方向。 这些物剂是随机地在一个宽广的环状区域上行进时或逆时针的。 我们以圆柱形上的“ 收缩” 相形轨迹为模型。 碰撞导致物剂改变其运动方向。 为避免这种情况, 代理人可能决定转换轨迹, 以便与朝着其方向行进的代理人排合并。 我们证明, 这些物剂最终必须聚集到关于运动方向的当地共识, 意味着每个窄轨迹上的所有物剂都必须最终向同一方向行进。 我们给预期的时间以“ 缩式框框框框框框 ”, 我们的轨迹的轨迹最终会显示轨道的轨迹的轨迹, 。