Quasi-polynomial Time Approximation of Output Probabilities of Constant-depth, Geometrically-local Quantum Circuits

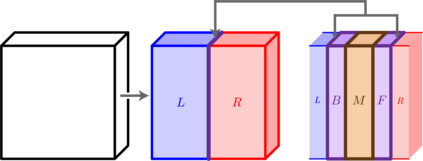
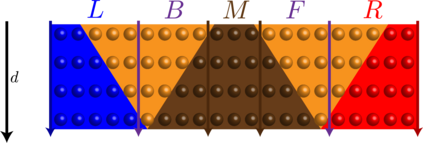
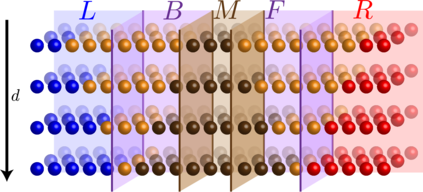
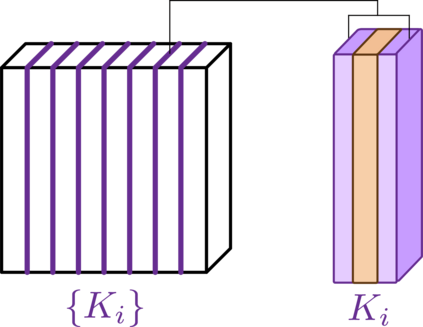
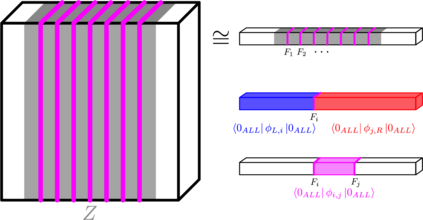
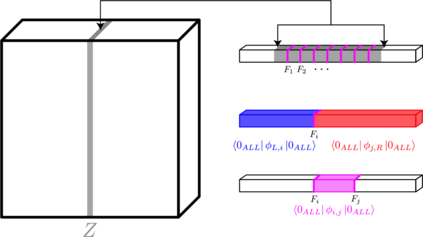
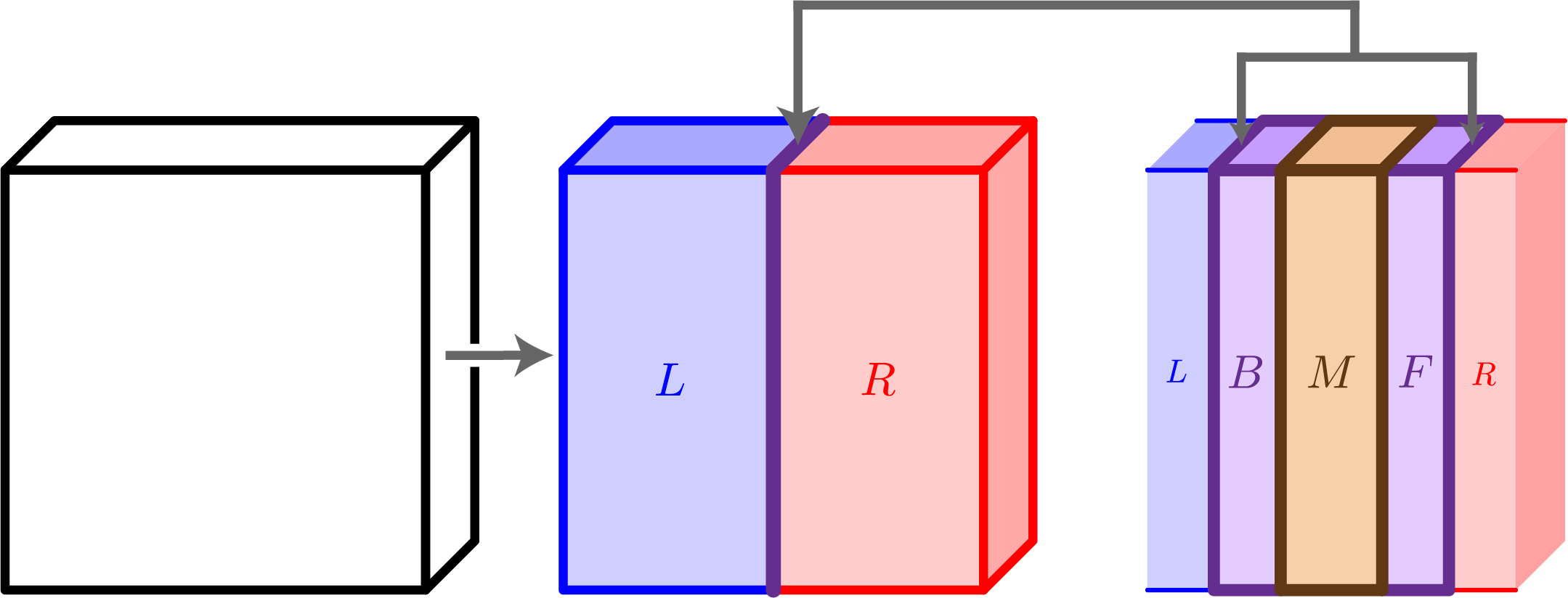
We present a classical algorithm that, for any 3D geometrically-local, constant-depth quantum circuit $C$, and any bit string $x \in \{0,1\}^n$, can compute the quantity $|<x|C |0^{\otimes n}>|^2$ to within any inverse-polynomial additive error in quasi-polynomial time. It is known that it is $\#P$-hard to compute this same quantity to within $2^{-n^2}$ additive error [Mov20]. The previous best known algorithm for this problem used $O(2^{n^{1/3}}\text{poly}(1/\epsilon))$ time to compute probabilities to within additive error $\epsilon$ [BGM20]. Notably, the [BGM20] paper included an elegant polynomial time algorithm for the same estimation task with 2D circuits, which makes a novel use of 1D Matrix Product States carefully tailored to the 2D geometry of the circuit in question. Surprisingly, it is not clear that it is possible to extend this use of MPS to address the case of 3D circuits in polynomial time. This raises a natural question as to whether the computational complexity of the 3D problem might be drastically higher than that of the 2D problem. In this work we address this question by exhibiting a quasi-polynomial time algorithm for the 3D case. In order to surpass the technical barriers encountered by previously known techniques we are forced to pursue a novel approach: Our algorithm has a Divide-and-Conquer structure, constructing a recursive sub-division of the given 3D circuit using carefully designed block-encodings, each creating a 3D-local circuit on at most half the number of qubits as the original. This division step is then applied recursively, expressing the original quantity as a weighted sum of smaller and smaller 3D-local quantum circuits. A central technical challenge is to control correlations arising from the entanglement that may exist between the different circuit "pieces" produced this way.