A conforming sliding mesh technique for an embedded-hybridized discontinuous Galerkin discretization for fluid-rigid body interaction

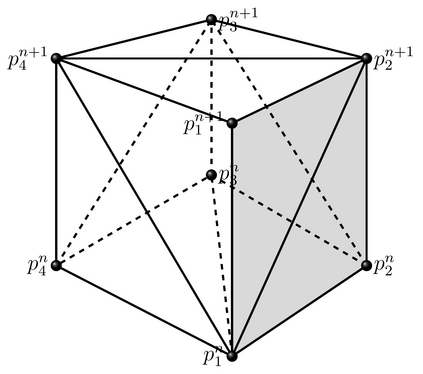
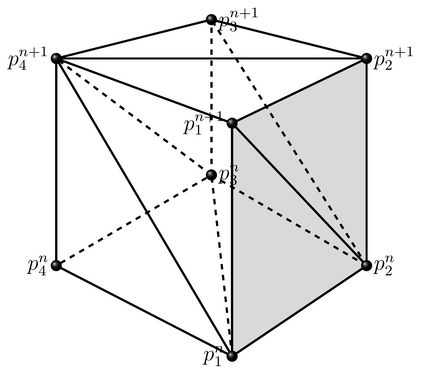
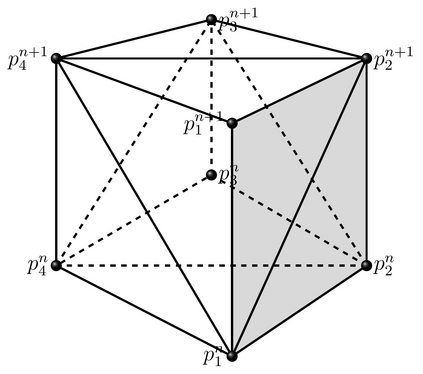
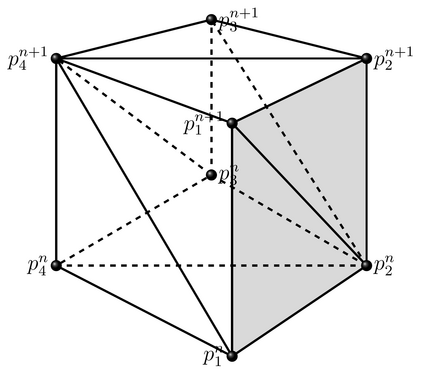
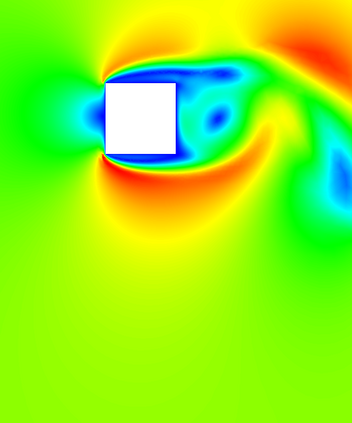
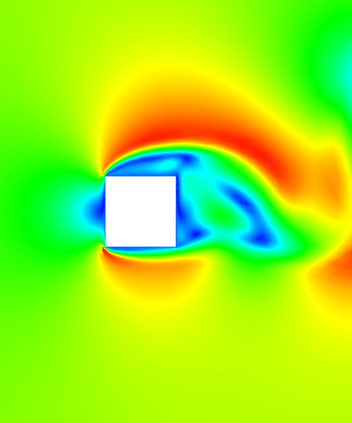
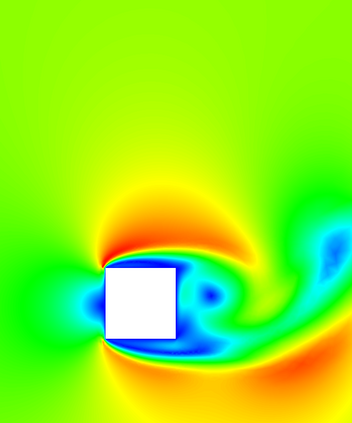
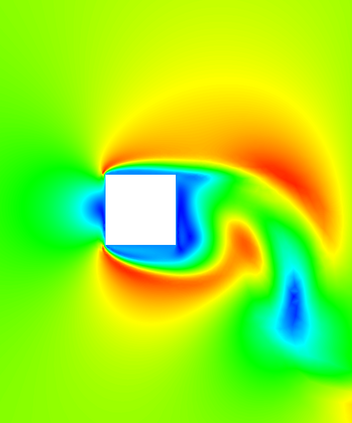
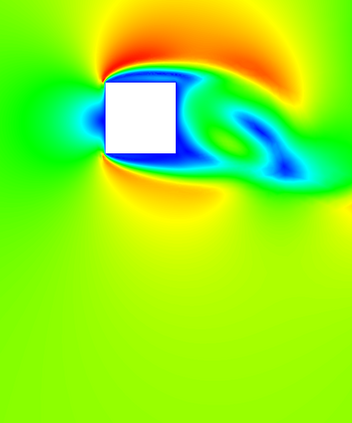
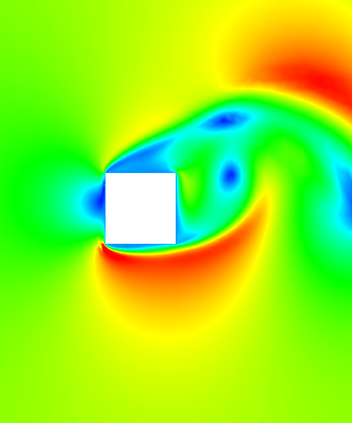
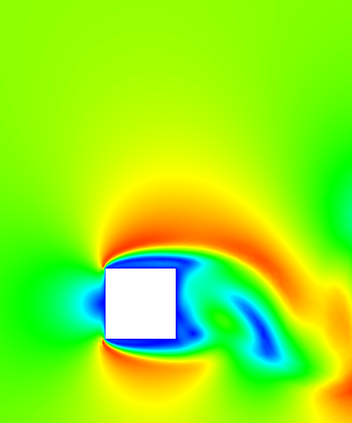
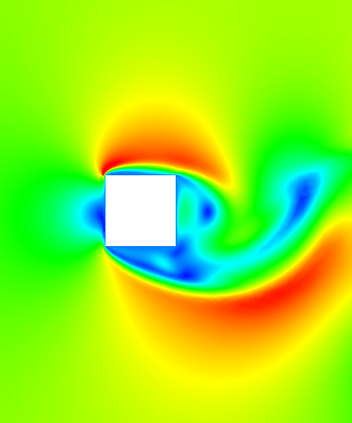
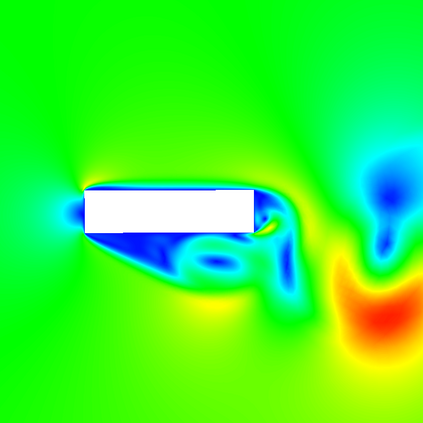
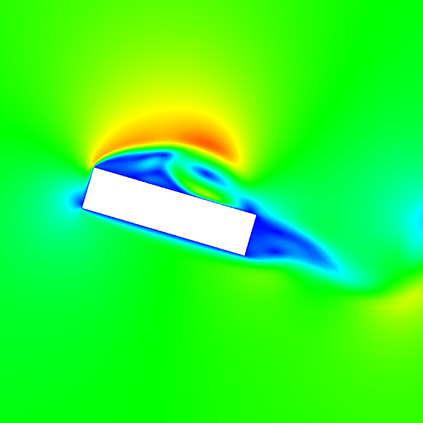
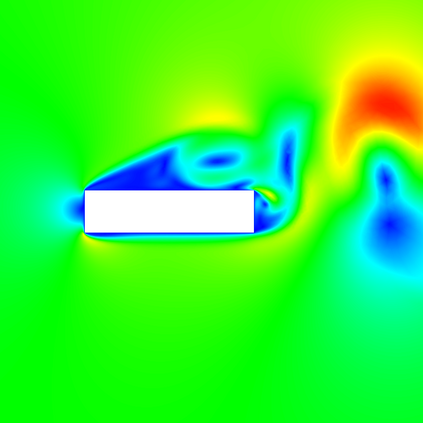
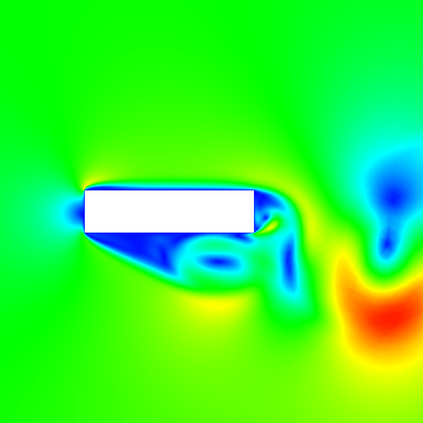
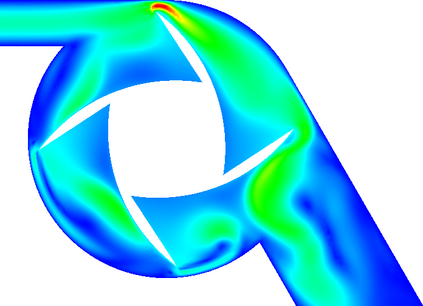
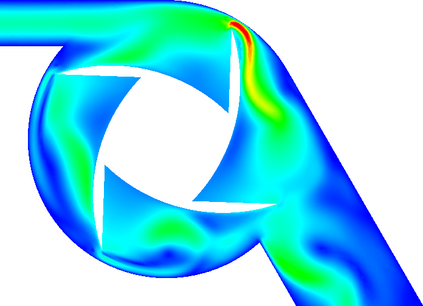
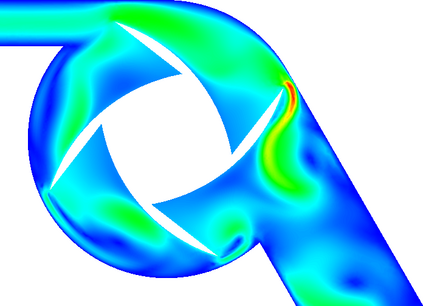
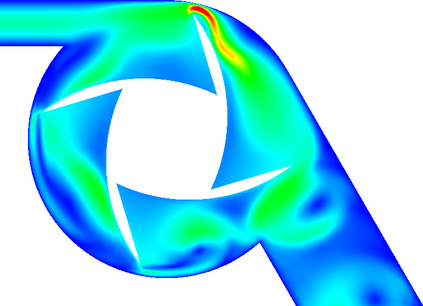
In (J. Comput. Phys., 417, 109577, 2020) we introduced a space-time embedded-hybridizable discontinuous Galerkin method for the solution of the incompressible Navier-Stokes equations on time-dependent domains of which the motion of the domain is prescribed. This discretization is exactly mass conserving, locally momentum conserving, and energy-stable. In this manuscript we extend this discretization to fluid-rigid body interaction problems in which the motion of the fluid domain is not known a priori. To account for large rotational motion of the rigid body, we present a novel conforming space-time sliding mesh technique. We demonstrate the performance of the discretization on various numerical examples.