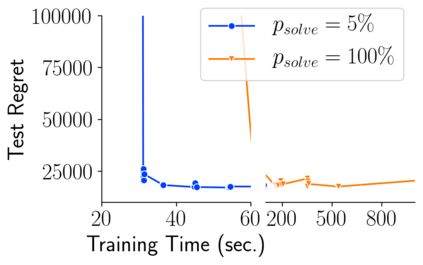
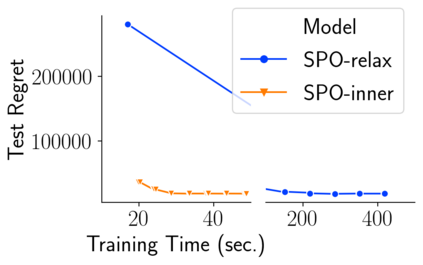
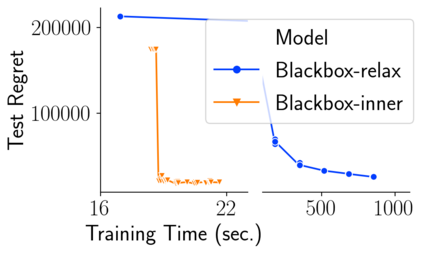
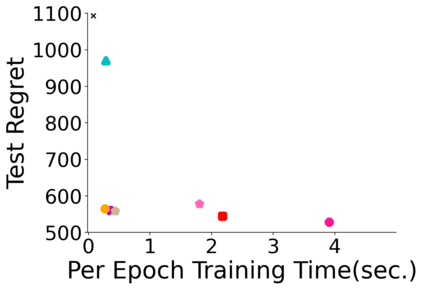
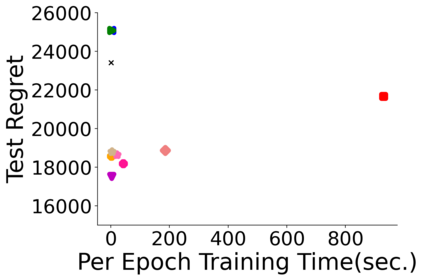
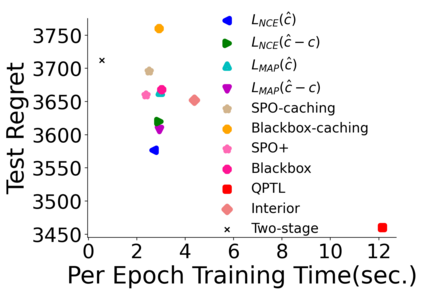
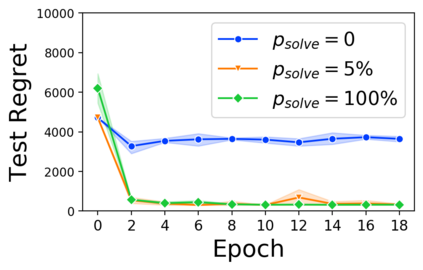
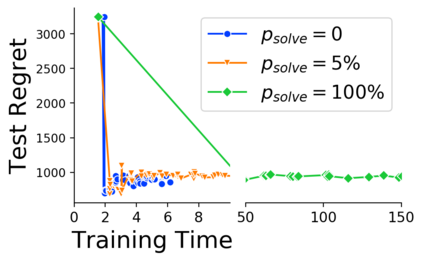
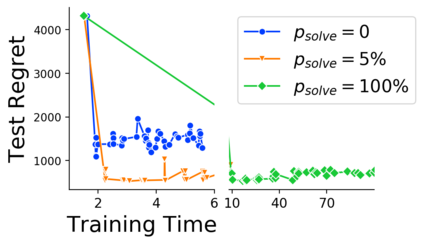
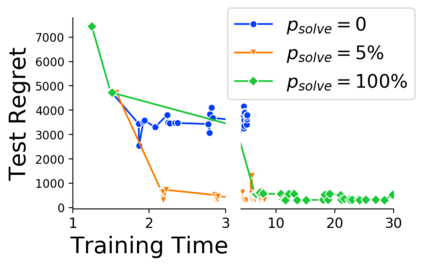
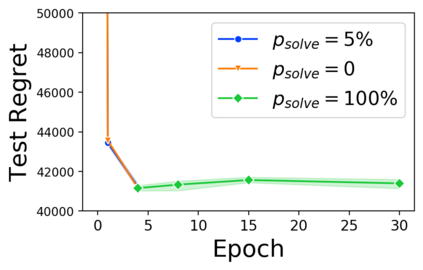
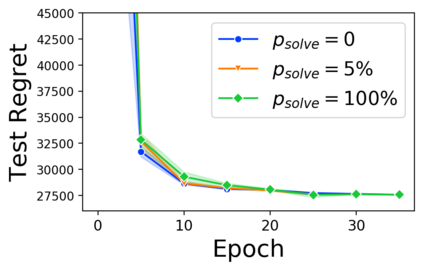
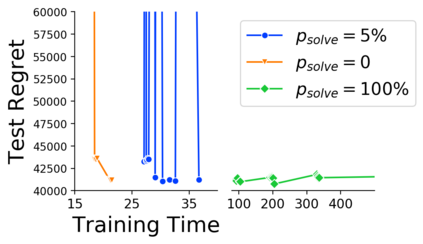
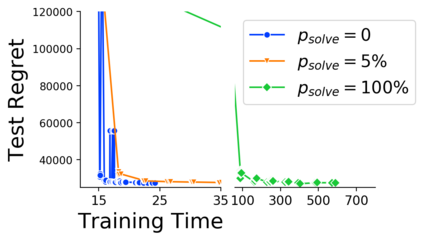
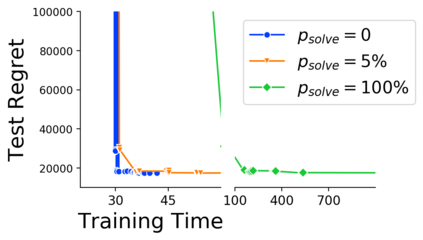
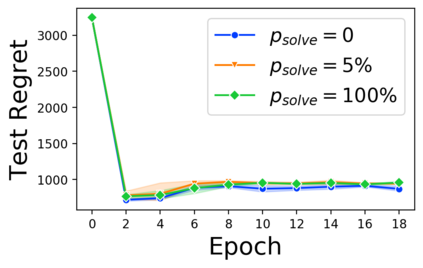
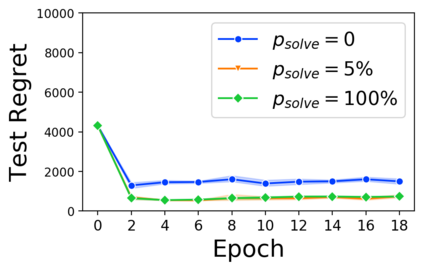
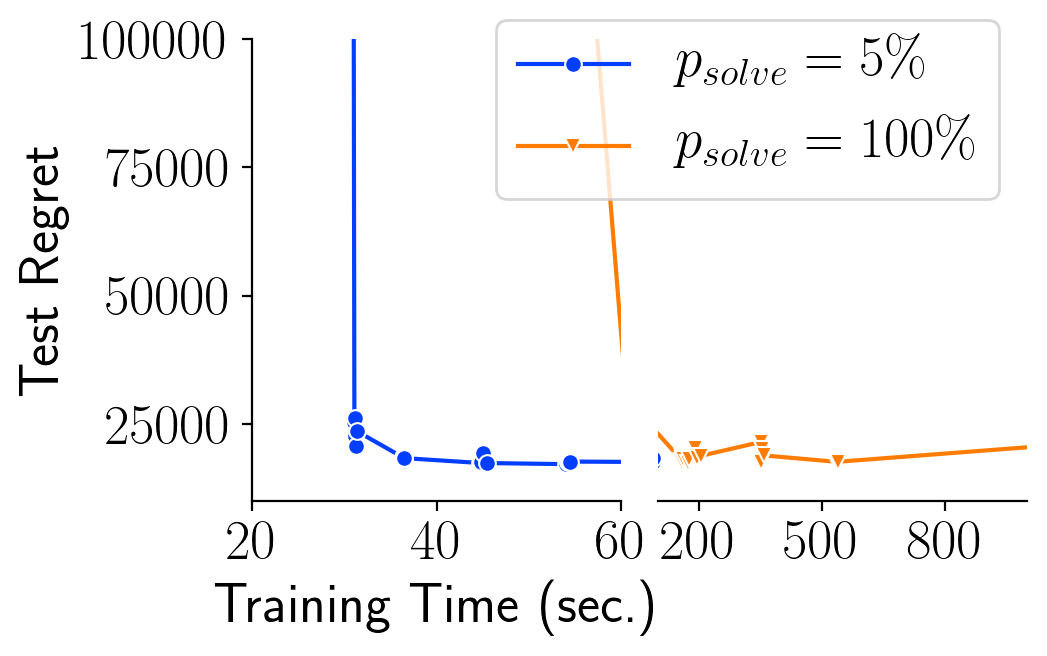
Many decision-making processes involve solving a combinatorial optimization problem with uncertain input that can be estimated from historic data. Recently, problems in this class have been successfully addressed via end-to-end learning approaches, which rely on solving one optimization problem for each training instance at every epoch. In this context, we provide two distinct contributions. First, we use a Noise Contrastive approach to motivate a family of surrogate loss functions, based on viewing non-optimal solutions as negative examples. Second, we address a major bottleneck of all predict-and-optimize approaches, i.e. the need to frequently recompute optimal solutions at training time. This is done via a solver-agnostic solution caching scheme, and by replacing optimization calls with a lookup in the solution cache. The method is formally based on an inner approximation of the feasible space and, combined with a cache lookup strategy, provides a controllable trade-off between training time and accuracy of the loss approximation. We empirically show that even a very slow growth rate is enough to match the quality of state-of-the-art methods, at a fraction of the computational cost.
翻译:许多决策过程涉及解决组合优化问题,其投入无法根据历史数据作出估计。最近,通过端到端学习方法成功地解决了这一类中的问题,这取决于在每个时代解决每个培训案例的一个优化问题。在这方面,我们提供两种截然不同的贡献。首先,我们根据将非最佳解决办法视为负面例子,用一个非最佳解决办法来激励代谢损失功能的大家庭。第二,我们解决了所有预测和优化方法的重大瓶颈,即需要经常在培训时间重新配置最佳解决办法。这是通过一个求解者-不可知解决方案缓冲办法,以及用解决方案缓存中的一个外观取代优化电话。这种方法正式以可行空间的内部近似为基础,加上缓存外观战略,在培训时间和损失近似准确性之间提供了一种可控制的交易。我们的经验显示,即使非常缓慢的增长率足以满足州级方法的质量,也是计算成本的一小部分。