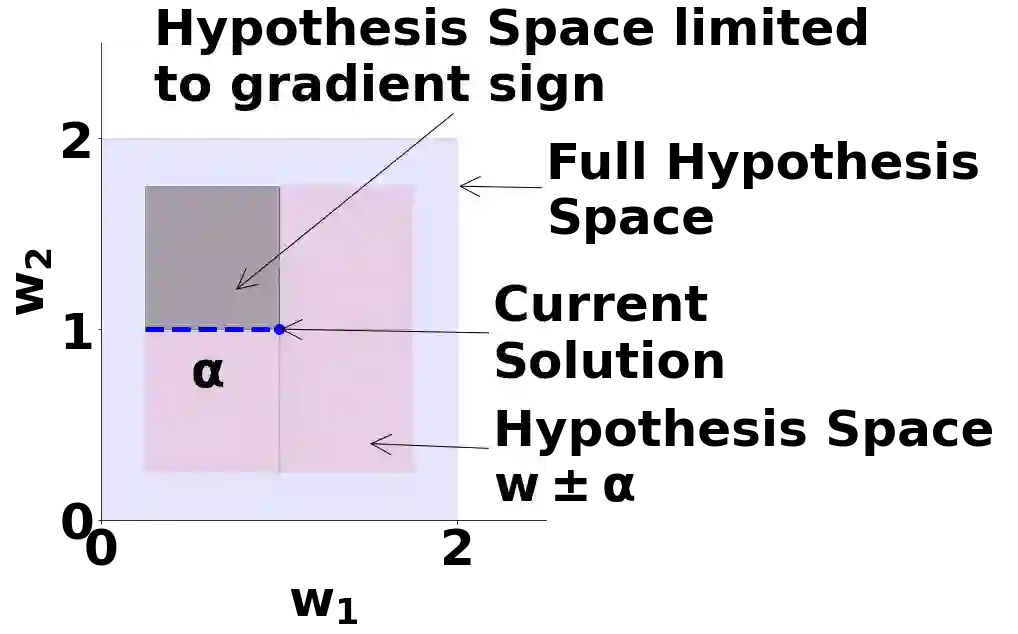
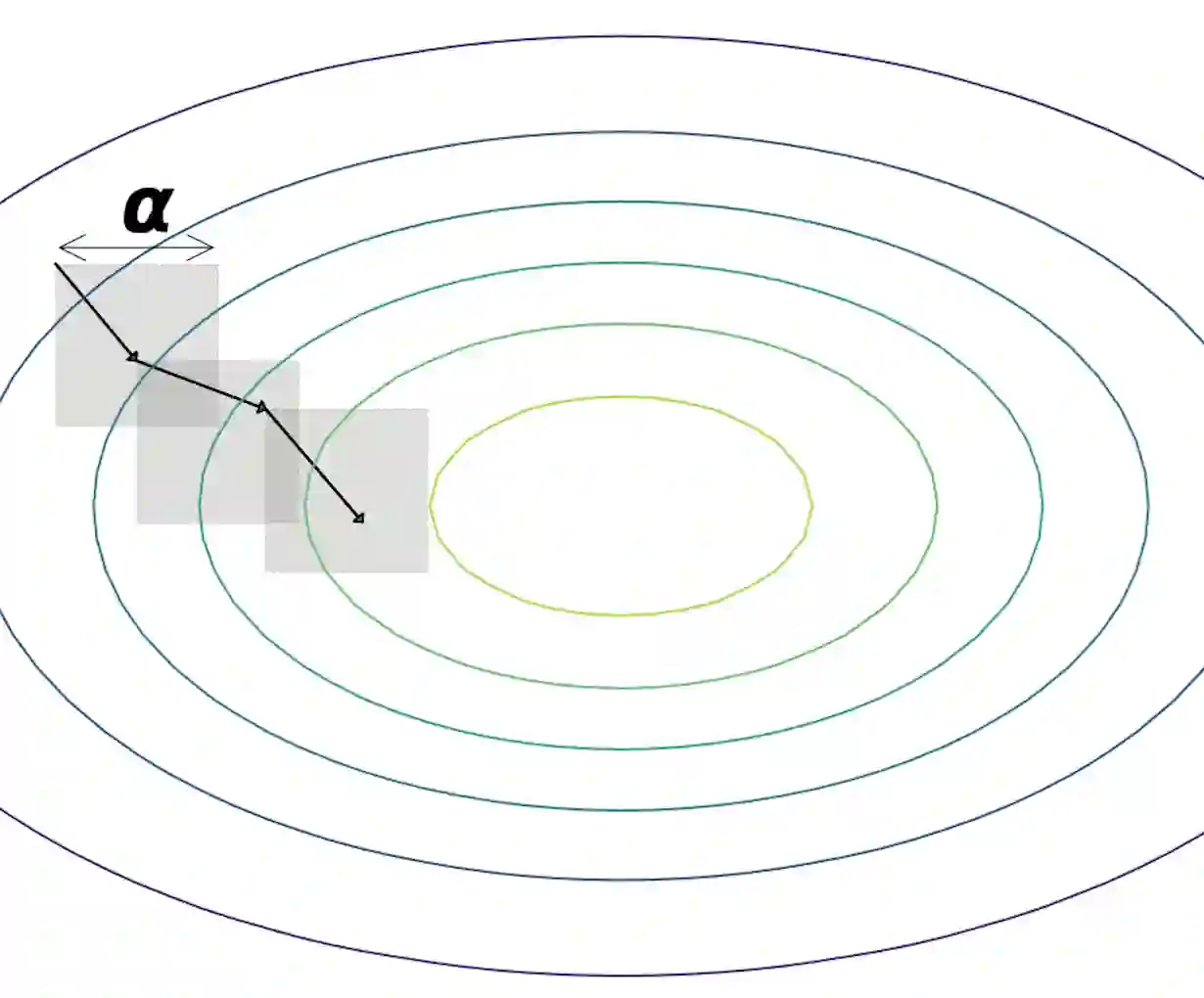
In many real world applications of machine learning, models have to meet certain domain-based requirements that can be expressed as constraints (e.g., safety-critical constraints in autonomous driving systems). Such constraints are often handled by including them in a regularization term, while learning a model. This approach, however, does not guarantee 100% satisfaction of the constraints: it only reduces violations of the constraints on the training set rather than ensuring that the predictions by the model will always adhere to them. In this paper, we present a framework for learning models that provably fulfil the constraints under all circumstances (i.e., also on unseen data). To achieve this, we cast learning as a maximum satisfiability problem, and solve it using a novel SaDe algorithm that combines constraint satisfaction with gradient descent. We compare our method against regularization based baselines on linear models and show that our method is capable of enforcing different types of domain constraints effectively on unseen data, without sacrificing predictive performance.
翻译:在机器学习的许多现实世界应用中,模型必须满足某些可以被表述为制约因素的基于领域的要求(如自主驾驶系统的安全关键限制),这些限制往往通过在学习模式的同时将其纳入正规化术语来处理,但这种方法并不能保证100%地满足这些限制:这只能减少对成套培训的限制,而不是确保模型的预测将始终遵守这些限制。在本文件中,我们提出了一个学习模式的框架,这些模式在各种情况下(例如,在不可见的数据方面)都可有效满足各种限制。为了做到这一点,我们把学习当作一个最大限度的可支配性问题,并使用将制约满意度与梯度下降相结合的新型Sade算法加以解决。我们比较了我们的方法,而不是基于线性模型的正规化基线,并表明我们的方法能够有效地对不可见的数据(即也是关于不可见的数据)实施不同类型的领域限制,同时不牺牲预测性能。