Quantum field-theoretic machine learning

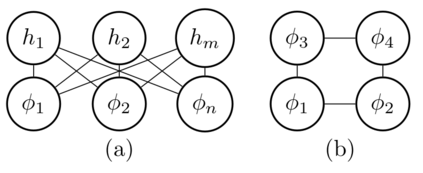
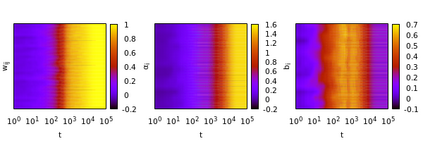
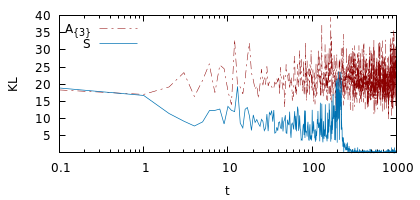
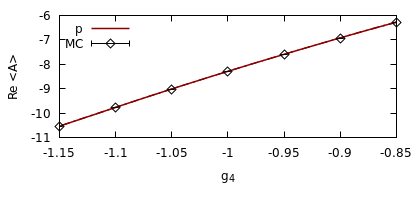
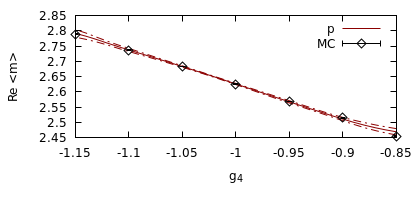
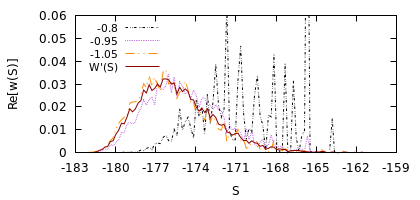
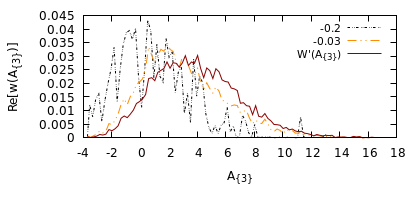
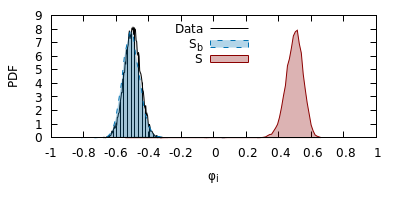
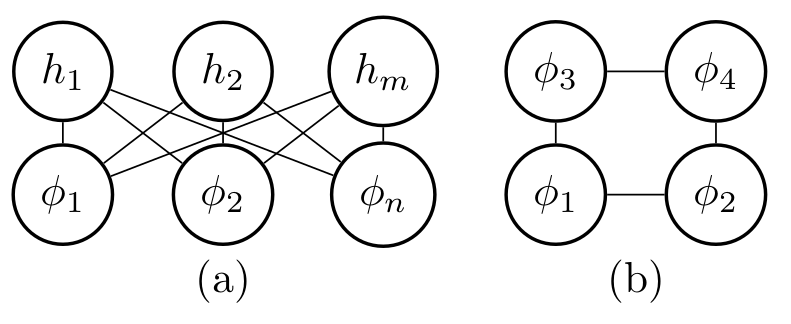
We derive machine learning algorithms from discretized Euclidean field theories, making inference and learning possible within dynamics described by quantum field theory. Specifically, we demonstrate that the $\phi^{4}$ scalar field theory satisfies the Hammersley-Clifford theorem, therefore recasting it as a machine learning algorithm within the mathematically rigorous framework of Markov random fields. We illustrate the concepts by minimizing an asymmetric distance between the probability distribution of the $\phi^{4}$ theory and that of target distributions, by quantifying the overlap of statistical ensembles between probability distributions and through reweighting to complex-valued actions with longer-range interactions. Neural networks architectures are additionally derived from the $\phi^{4}$ theory which can be viewed as generalizations of conventional neural networks and applications are presented. We conclude by discussing how the proposal opens up a new research avenue, that of developing a mathematical and computational framework of machine learning within quantum field theory.