Best Arm Identification with a Fixed Budget under a Small Gap

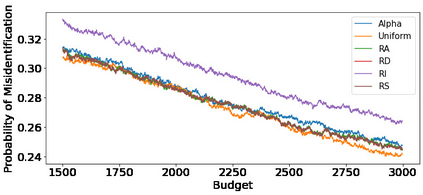
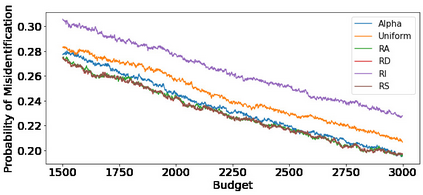
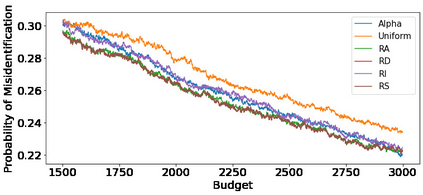
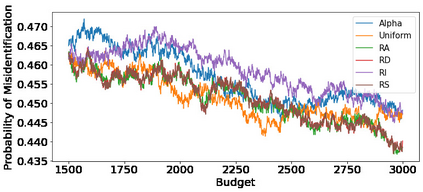
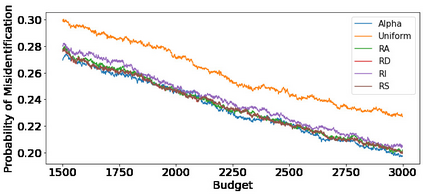
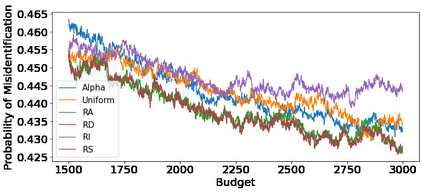
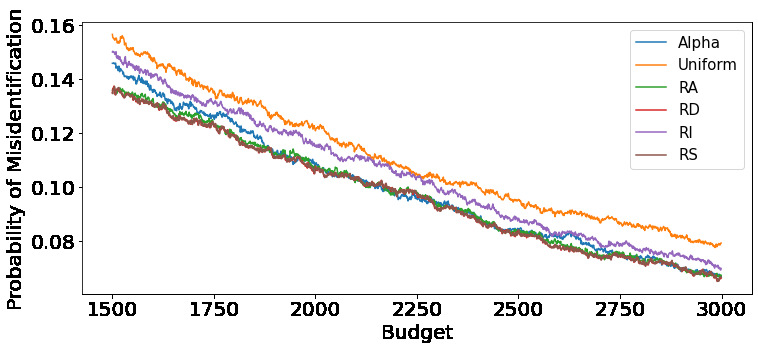
We consider the fixed-budget best arm identification problem in the multi-armed bandit problem. One of the main interests in this field is to derive a tight lower bound on the probability of misidentifying the best arm and to develop a strategy whose performance guarantee matches the lower bound. However, it has long been an open problem when the optimal allocation ratio of arm draws is unknown. In this paper, we provide an answer for this problem under which the gap between the expected rewards is small. First, we derive a tight problem-dependent lower bound, which characterizes the optimal allocation ratio that depends on the gap of the expected rewards and the Fisher information of the bandit model. Then, we propose the "RS-AIPW" strategy, which consists of the randomized sampling (RS) rule using the estimated optimal allocation ratio and the recommendation rule using the augmented inverse probability weighting (AIPW) estimator. Our proposed strategy is optimal in the sense that the performance guarantee achieves the derived lower bound under a small gap. In the course of the analysis, we present a novel large deviation bound for martingales.