Hamiltonian Operator Inference: Physics-preserving Learning of Reduced-order Models for Hamiltonian Systems

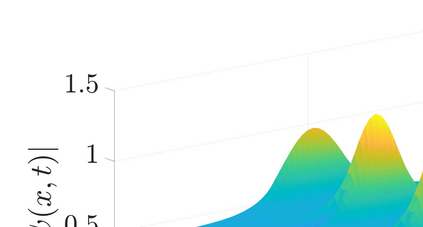
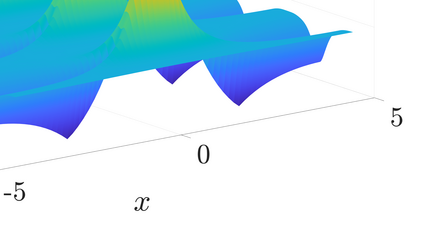
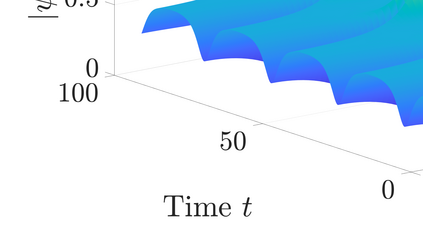
This work presents a nonintrusive physics-preserving method to learn reduced-order models (ROMs) of Hamiltonian systems. Traditional intrusive projection-based model reduction approaches utilize symplectic Galerkin projection to construct Hamiltonian reduced models by projecting Hamilton's equations of the full model onto a symplectic subspace. This symplectic projection requires complete knowledge about the full model operators and full access to manipulate the computer code. In contrast, the proposed Hamiltonian operator inference approach embeds the physics into the operator inference framework to develop a data-driven model reduction method that preserves the underlying symplectic structure. Our method exploits knowledge of the Hamiltonian functional to define and parametrize a Hamiltonian ROM form which can then be learned from data projected via symplectic projectors. The proposed method is `gray-box' in that it utilizes knowledge of the Hamiltonian structure at the partial differential equation level, as well as knowledge of spatially local components in the system. However, it does not require access to computer code, only data to learn the models. Our numerical results demonstrate Hamiltonian operator inference on a linear wave equation, the cubic nonlinear Schr\"{o}dinger equation, and a nonpolynomial sine-Gordon equation. Accurate long-time predictions far outside the training time interval for nonlinear examples illustrate the generalizability of our learned models.