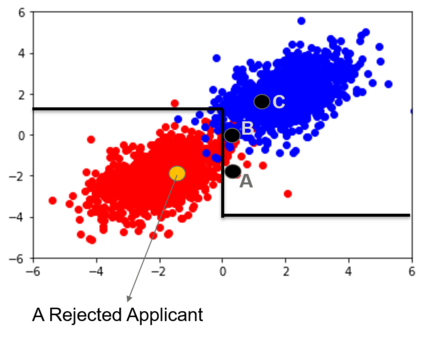
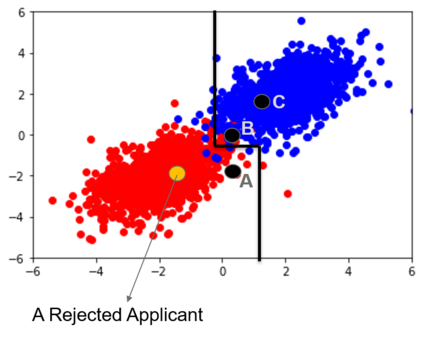
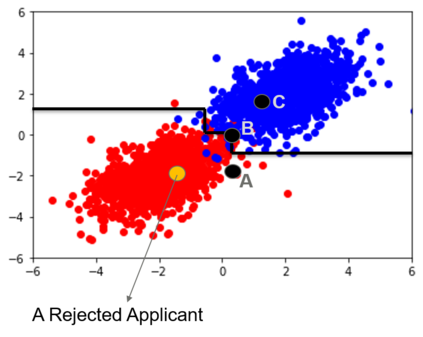
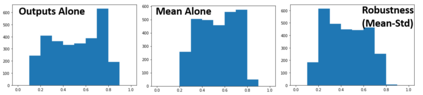
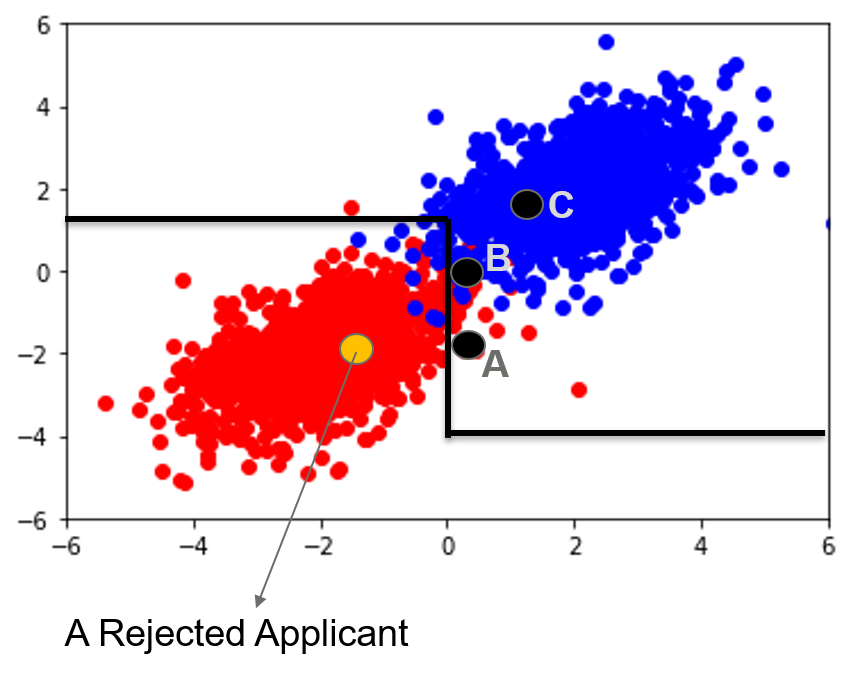
Counterfactual explanations inform ways to achieve a desired outcome from a machine learning model. However, such explanations are not robust to certain real-world changes in the underlying model (e.g., retraining the model, changing hyperparameters, etc.), questioning their reliability in several applications, e.g., credit lending. In this work, we propose a novel strategy -- that we call RobX -- to generate robust counterfactuals for tree-based ensembles, e.g., XGBoost. Tree-based ensembles pose additional challenges in robust counterfactual generation, e.g., they have a non-smooth and non-differentiable objective function, and they can change a lot in the parameter space under retraining on very similar data. We first introduce a novel metric -- that we call Counterfactual Stability -- that attempts to quantify how robust a counterfactual is going to be to model changes under retraining, and comes with desirable theoretical properties. Our proposed strategy RobX works with any counterfactual generation method (base method) and searches for robust counterfactuals by iteratively refining the counterfactual generated by the base method using our metric Counterfactual Stability. We compare the performance of RobX with popular counterfactual generation methods (for tree-based ensembles) across benchmark datasets. The results demonstrate that our strategy generates counterfactuals that are significantly more robust (nearly 100% validity after actual model changes) and also realistic (in terms of local outlier factor) over existing state-of-the-art methods.
翻译:反事实解释为从机器学习模式中获得理想结果提供了信息。然而,这种解释对于基础模型中某些真实世界的变化(例如,模型再培训、改变超参数等)并不有力,质疑其在若干应用中的可靠性,例如信用贷款。在这项工作中,我们提出了一个新颖的战略 -- -- 我们称之为RobX -- -- 为基于树木的组合产生强有力的反事实,例如,XGBoost。基于树木的组合在强大的反事实生成方面构成额外的挑战,例如,它们具有非模拟和不可区别的目标功能,而且它们可以在非常相似的数据再培训中改变许多参数空间。我们首先引入了一个新的指标 -- -- 我们称之为反事实稳定 -- -- 试图量化一个有力的反事实将变成在再培训中的模型,并带有理想的理论属性。我们提议的RobX战略与任何反事实生成方法(基准方法)合作,通过对真实现实数据进行反复的修改来寻找坚实的反事实数据。我们用现有数据模型对真实性数据进行对比后,我们用现有的标准进行对比。