Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge Equivariant Projected Kernels

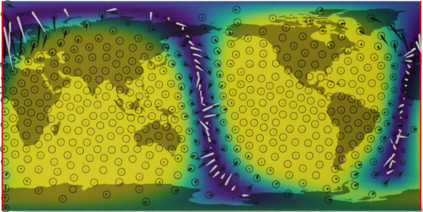
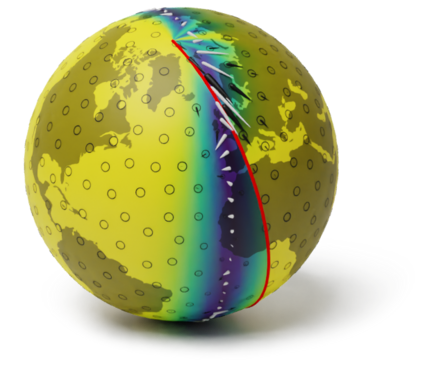
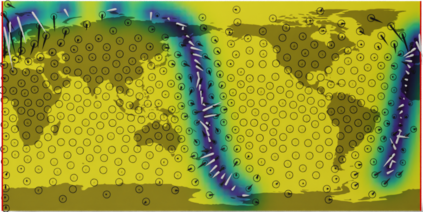
Gaussian processes are machine learning models capable of learning unknown functions in a way that represents uncertainty, thereby facilitating construction of optimal decision-making systems. Motivated by a desire to deploy Gaussian processes in novel areas of science, a rapidly-growing line of research has focused on constructively extending these models to handle non-Euclidean domains, including Riemannian manifolds, such as spheres and tori. We propose techniques that generalize this class to model vector fields on Riemannian manifolds, which are important in a number of application areas in the physical sciences. To do so, we present a general recipe for constructing gauge equivariant kernels, which induce Gaussian vector fields, i.e. vector-valued Gaussian processes coherent with geometry, from scalar-valued Riemannian kernels. We extend standard Gaussian process training methods, such as variational inference, to this setting. This enables vector-valued Gaussian processes on Riemannian manifolds to be trained using standard methods and makes them accessible to machine learning practitioners.