UWB-based Target Localization using Adaptive Belief Propagation in the HMM Framework

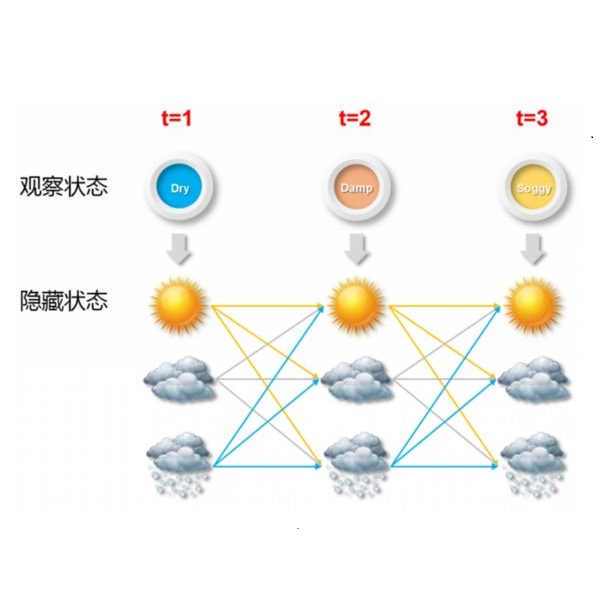
This paper proposes a novel adaptive sample space-based Viterbi algorithm for ultra-wideband (UWB) based target localization in an online manner. As the discretized area of interest is defined as a finite number of hidden states, the most probable trajectory of the unspecified agent is computed efficiently via dynamic programming in a Hidden Markov Model (HMM) framework. Furthermore, the approach has no requirements about Gaussian assumption and linearization for Bayesian calculation. However, the issue of computational complexity becomes very critical as the number of hidden states increases for estimation accuracy and large space. Previous localization works, based on discrete-state HMM, handle a small number of hidden variables, which represent specific paths or places. Inspired by the k-d Tree algorithm (e.g., quadtree) that is commonly used in the computer vision field, we propose a belief propagation in the most probable belief space with a low to high-resolution sequentially, thus reducing the required resources significantly. Our method has three advantages for localization: (a) no Gaussian assumptions and linearization, (b) handling the whole area of interest, not specific or small map representations, (c) reducing computation time and required memory size. Experimental tests demonstrate our results.