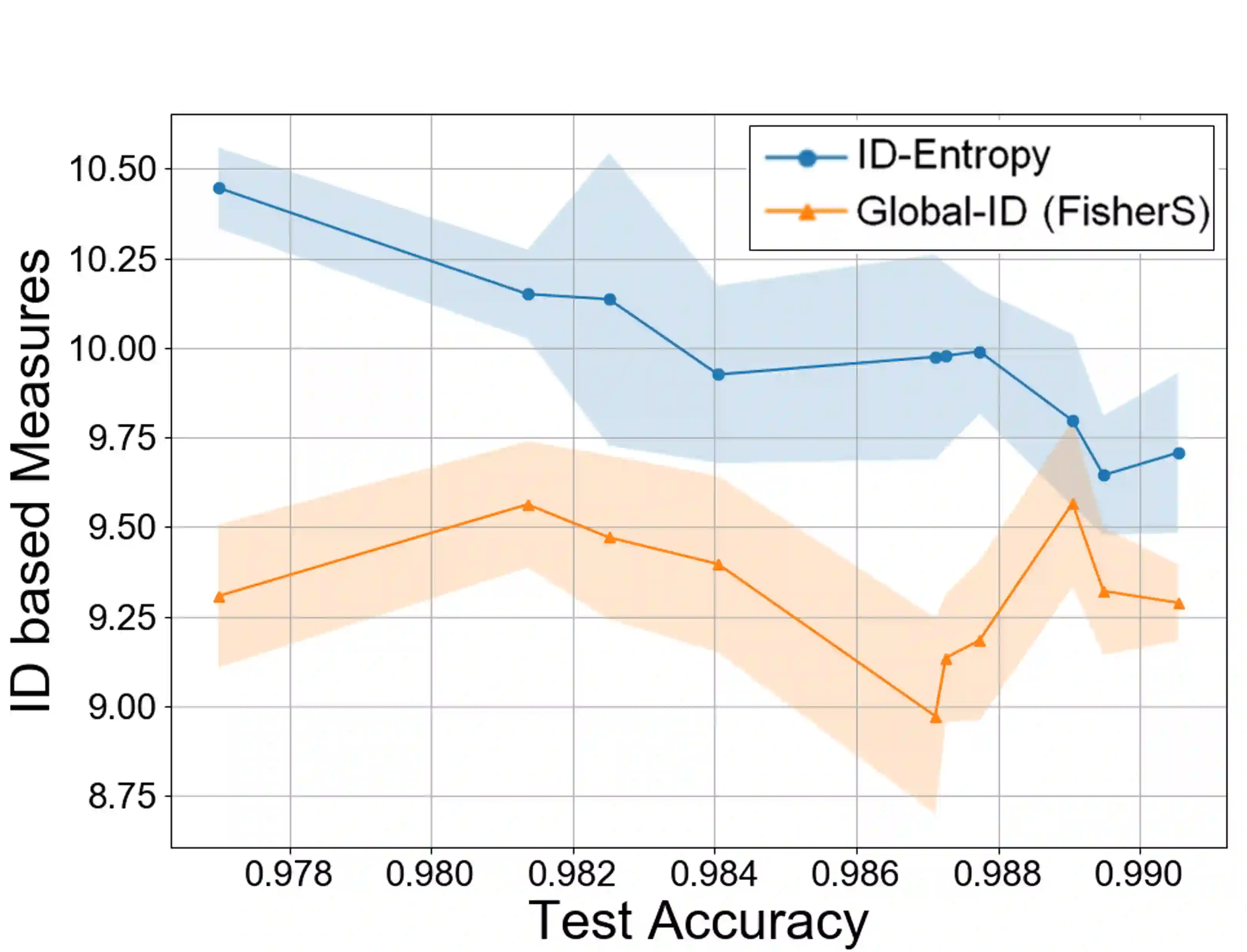
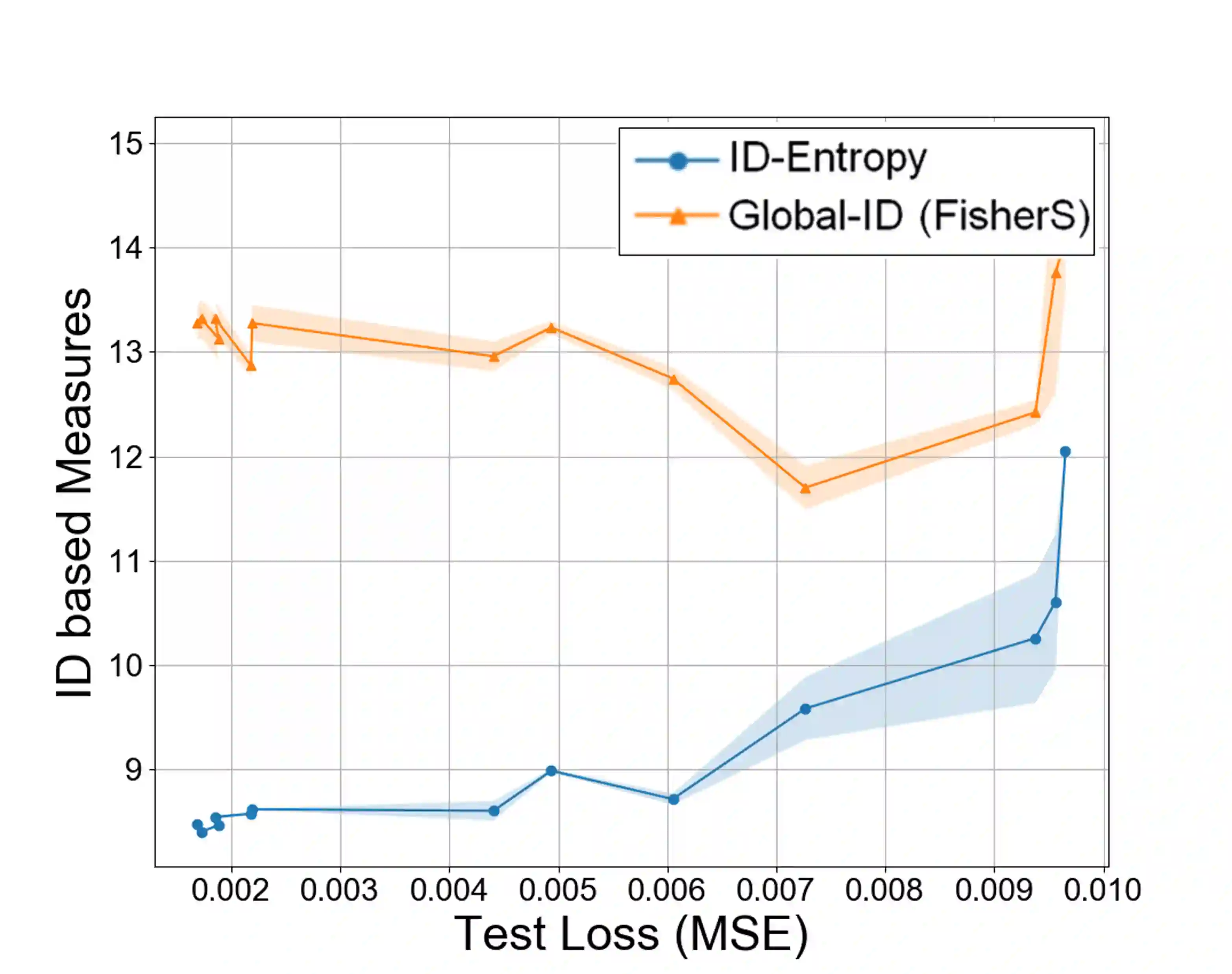
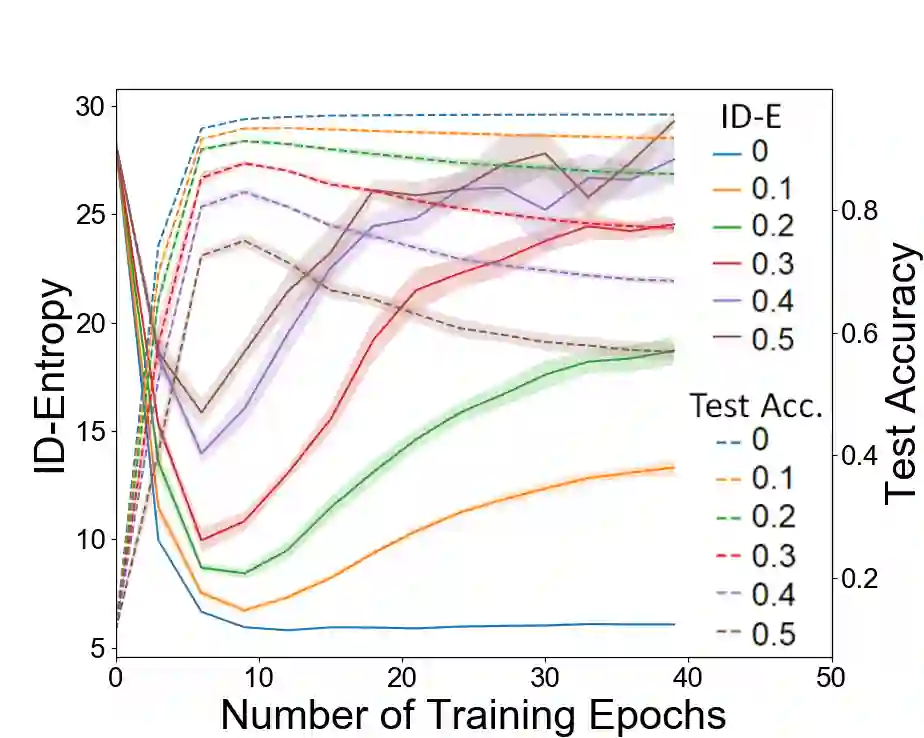
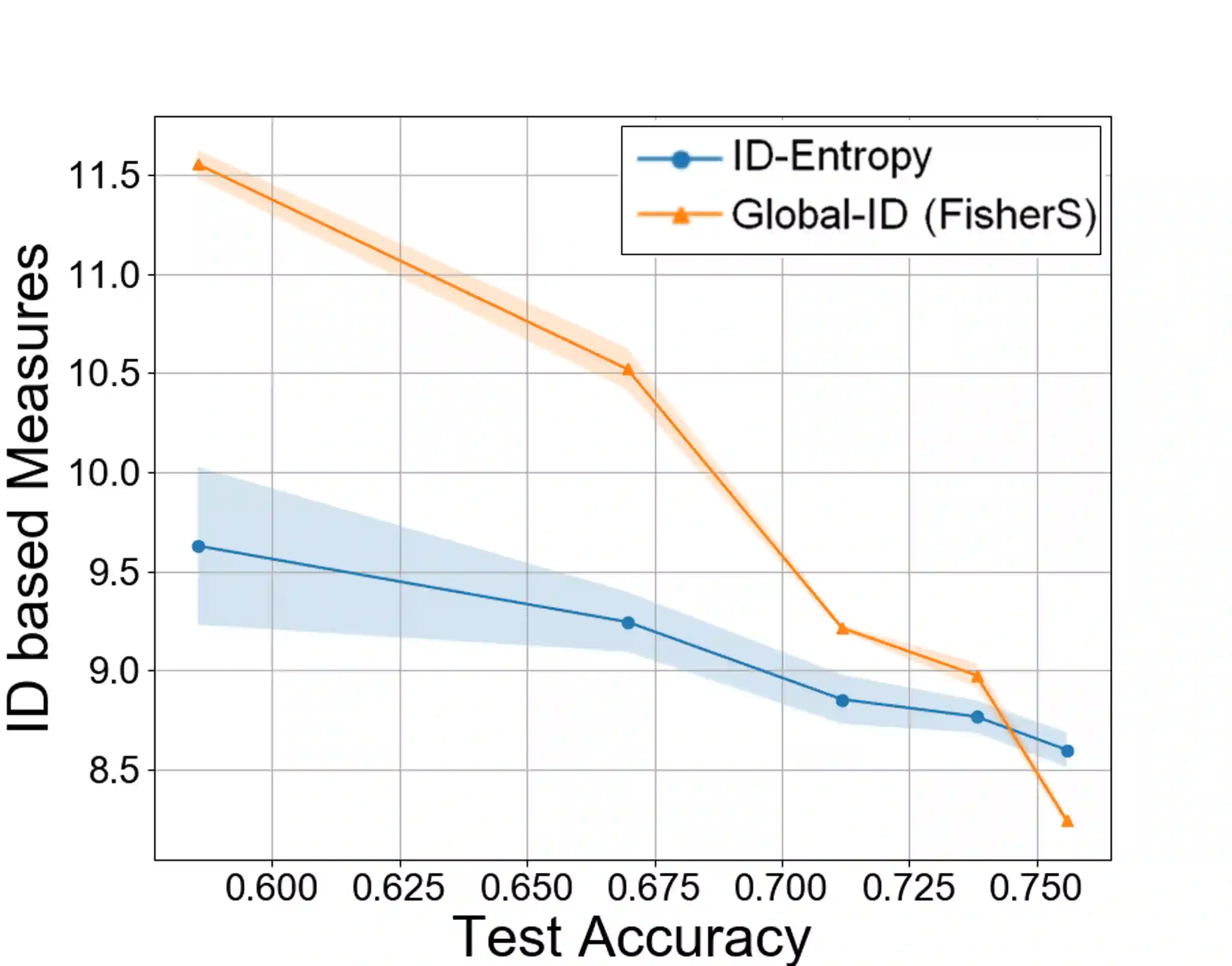
Most entropy measures depend on the spread of the probability distribution over the sample space X, and the maximum entropy achievable scales proportionately with the sample space cardinality |X|. For a finite |X|, this yields robust entropy measures which satisfy many important properties, such as invariance to bijections, while the same is not true for continuous spaces (where |X|=infinity). Furthermore, since R and R^d (d in Z+) have the same cardinality (from Cantor's correspondence argument), cardinality-dependent entropy measures cannot encode the data dimensionality. In this work, we question the role of cardinality and distribution spread in defining entropy measures for continuous spaces, which can undergo multiple rounds of transformations and distortions, e.g., in neural networks. We find that the average value of the local intrinsic dimension of a distribution, denoted as ID-Entropy, can serve as a robust entropy measure for continuous spaces, while capturing the data dimensionality. We find that ID-Entropy satisfies many desirable properties and can be extended to conditional entropy, joint entropy and mutual-information variants. ID-Entropy also yields new information bottleneck principles and also links to causality. In the context of deep learning, for feedforward architectures, we show, theoretically and empirically, that the ID-Entropy of a hidden layer directly controls the generalization gap for both classifiers and auto-encoders, when the target function is Lipschitz continuous. Our work primarily shows that, for continuous spaces, taking a structural rather than a statistical approach yields entropy measures which preserve intrinsic data dimensionality, while being relevant for studying various architectures.
翻译:大多数熵度量取决于概率分布在样本空间X上的展布情况,可达到的最大熵与样本空间基数|X|成比例。对于有限|X|,这产生了具有鲁棒性的熵度量,符合许多重要特性,例如对双射的不变性,而在连续空间中(其中|X|=无穷大),同样不成立。此外,由于R和R^d(d在Z +中)具有相同的基数(来自Cantor的对应论证),基数相关的熵度量无法编码数据维度。在这项工作中,我们质疑了基数和分布展布在为连续空间定义熵度量中的作用,这些连续空间可以经历多轮变换和扭曲,例如在神经网络中。我们发现,分布的局部固有维度的平均值,表示为ID-Entropy,可以作为连续空间的鲁棒熵度量,同时捕捉数据维度。我们发现,ID-Entropy满足许多理想特性,并且可以扩展为条件熵,联合熵和互信息变体。ID-Entropy还产生了新的信息瓶颈原理,并与因果性相关联。在深度学习的背景下,对于前馈架构,我们理论上和经验上表明,当目标函数为Lipschitz连续时,隐藏层的ID-Entropy直接控制分类器和自编码器的泛化间隙。我们的工作主要表明,在连续空间中,采用结构性而不是统计性的方法可产生保持内在数据维度的熵度量,同时对于研究各种体系结构具有相关性。