Ricci flow-guided autoencoders in learning time-dependent dynamics

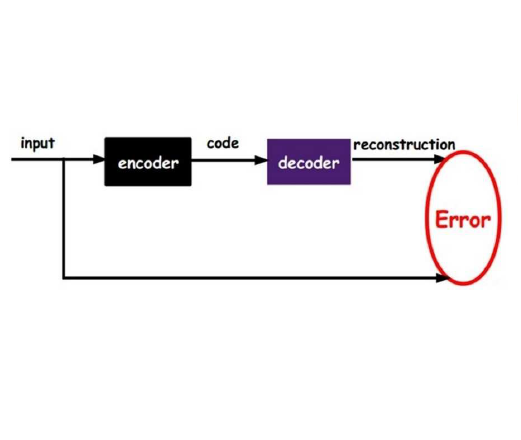
We present a manifold-based autoencoder method for learning dynamics in time, notably partial differential equations (PDEs), in which the manifold latent space evolves according to Ricci flow. This can be accomplished by parameterizing the latent manifold stage and subsequently simulating Ricci flow in a physics-informed setting, matching manifold quantities so that Ricci flow is empirically achieved. We emphasize dynamics that admit low-dimensional representations. With our method, the manifold, induced by the metric, is discerned through the training procedure, while the latent evolution due to Ricci flow provides an accommodating representation. By use of this flow, we sustain a canonical manifold latent representation for all values in the ambient PDE time interval continuum. We showcase that the Ricci flow facilitates qualities such as learning for out-of-distribution data and adversarial robustness on select PDE data. Moreover, we provide a thorough expansion of our methods in regard to special cases, such as neural discovery of non-parametric geometric flows based on conformally flat metrics with entropic strategies from Ricci flow theory.