An extension of the Unified Skew-Normal family of distributions and application to Bayesian binary regression

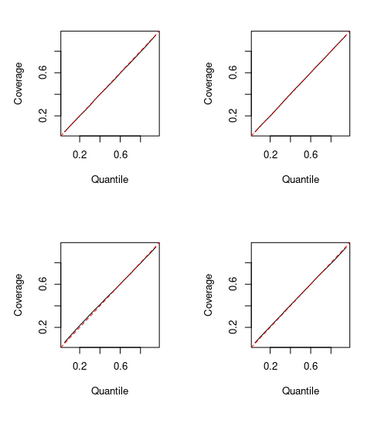
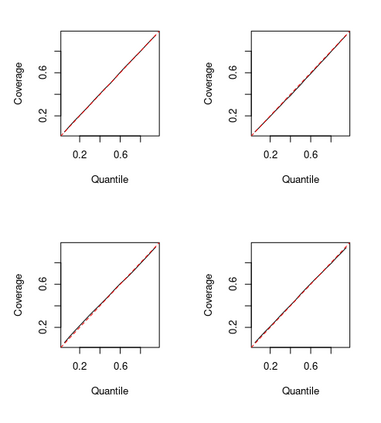
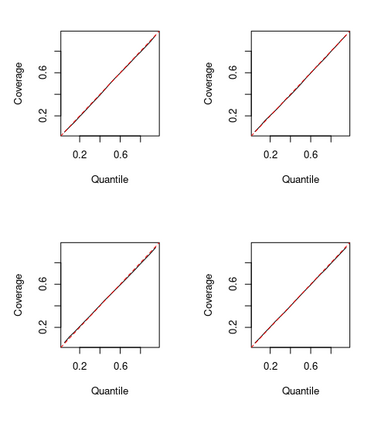
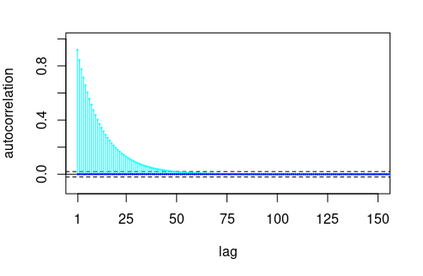
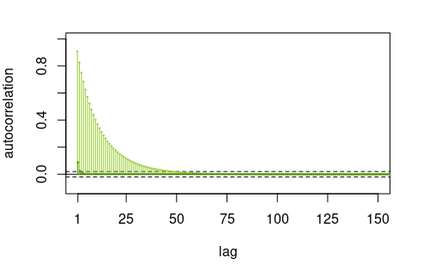
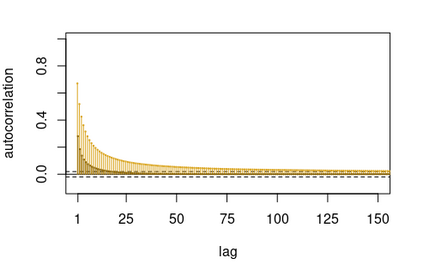
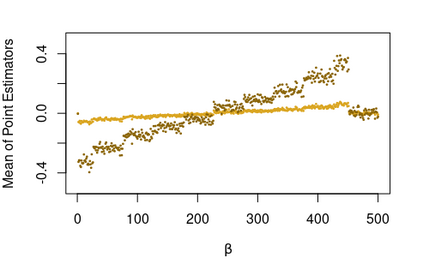
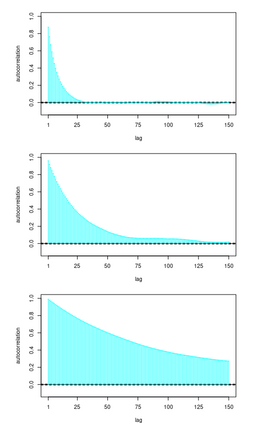
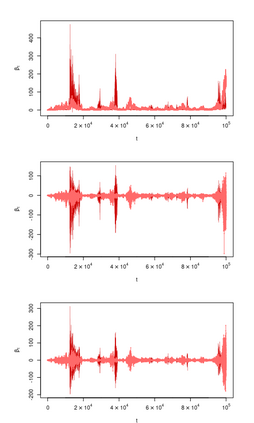
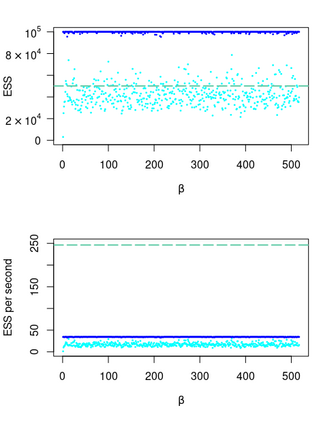
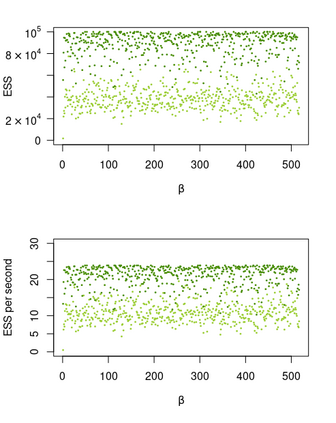
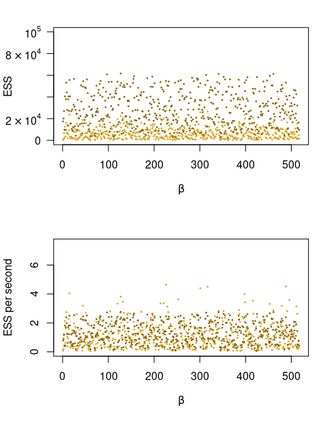
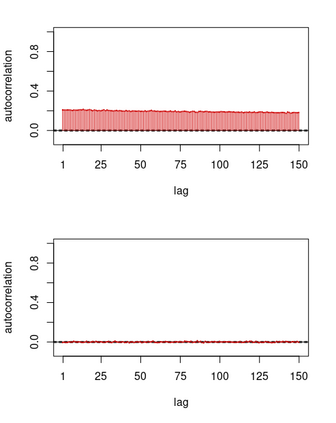
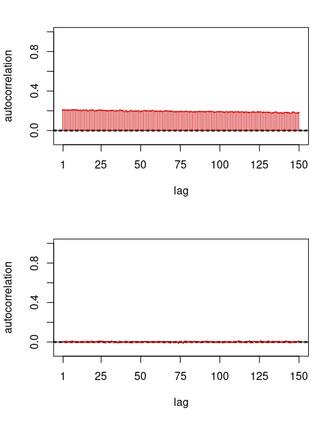
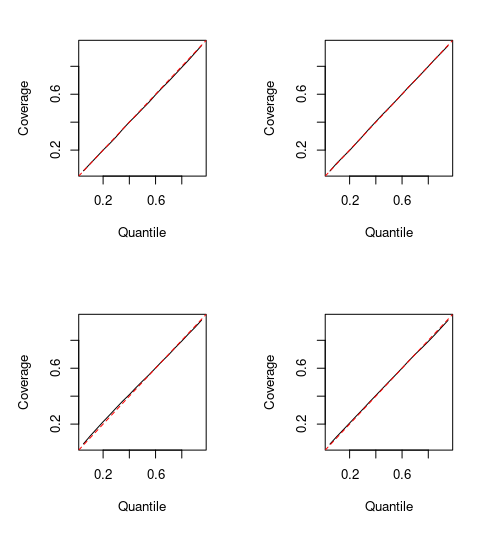
We consider the general problem of Bayesian binary regression and we introduce a new class of distributions, the Perturbed Unified Skew Normal (pSUN, henceforth), which generalizes the Unified Skew-Normal (SUN) class. We show that the new class is conjugate to any binary regression model, provided that the link function may be expressed as a scale mixture of Gaussian densities. We discuss in detail the popular logit case, and we show that, when a logistic regression model is combined with a Gaussian prior, posterior summaries such as cumulants and normalizing constants can be easily obtained through the use of an importance sampling approach, opening the way to straightforward variable selection procedures. For more general priors, the proposed methodology is based on a simple Gibbs sampler algorithm. We also claim that, in the p > n case, the proposed methodology shows better performances - both in terms of mixing and accuracy - compared to the existing methods. We illustrate the performance through several simulation studies and two data analyses.