Optimal Window Queries on Line Segments using the Trapezoidal Search DAG

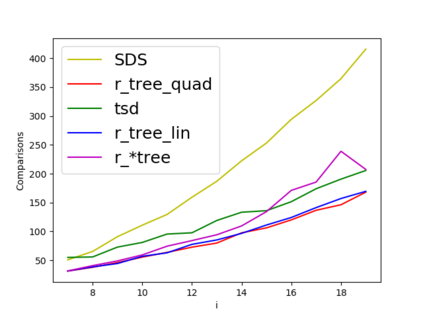
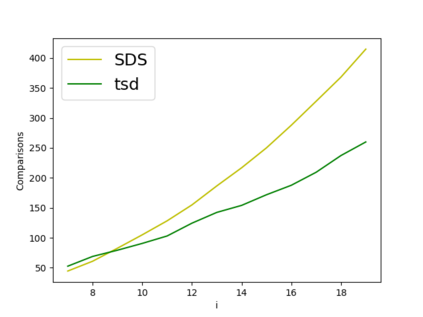
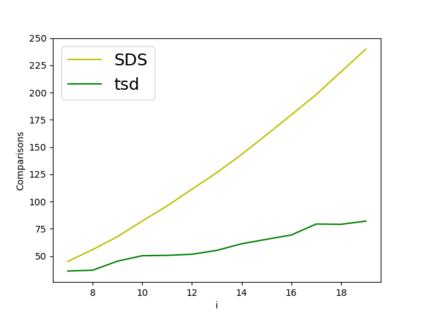
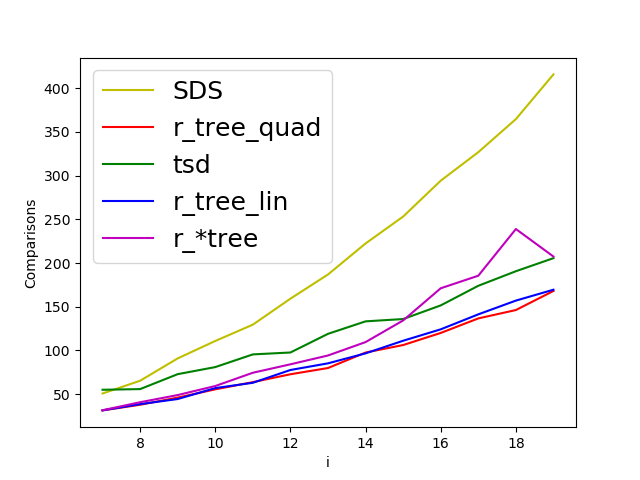
We propose new query applications of the well-known Trapezoidal Search DAG (TSD) on a set of $n$ line segments in the plane, where queries are allowed to be {\em vertical line segments}. We show that our algorithm reports the $k$ trapezoids that are intersected by the query segment in ${\cal O}(k+\log n)$ expected time, regardless of the spatial location of the segment set and the query. This improves on the query time and space bound of the well-known Segment Tree based approach, which is to date the theoretical bottleneck for optimal query time. In the case where the set of segments is a connected planar subdivision, this method can easily be extended to report the $k$ segments which intersect an axis aligned query window in ${\cal O}(k + \log n)$ expected time. Our publicly available implementation handles degeneracies exactly, including segments with overlap and multi-intersections. Experiments on real and synthetic data sets show that the method is practical and provides more reliable query times in comparison to R-trees and the segment tree based data structure.