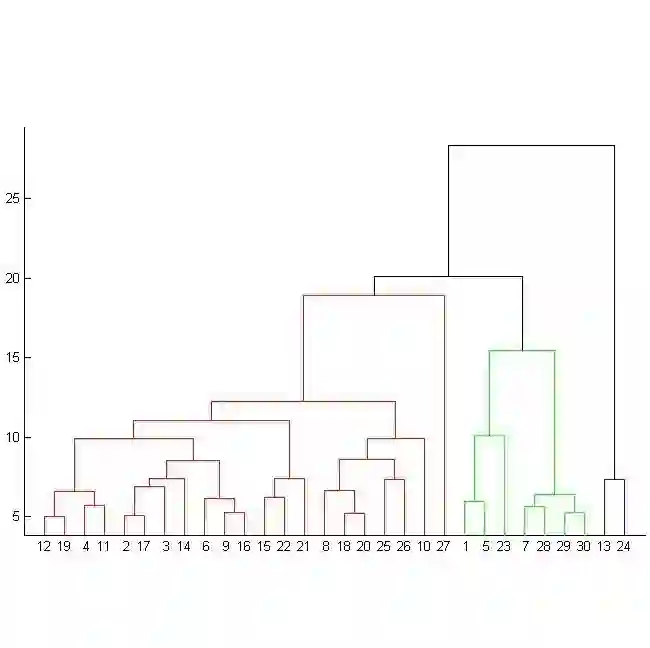
This paper studies the hierarchical clustering problem, where the goal is to produce a dendrogram that represents clusters at varying scales of a data set. We propose the ParChain framework for designing parallel hierarchical agglomerative clustering (HAC) algorithms, and using the framework we obtain novel parallel algorithms for the complete linkage, average linkage, and Ward's linkage criteria. Compared to most previous parallel HAC algorithms, which require quadratic memory, our new algorithms require only linear memory, and are scalable to large data sets. ParChain is based on our parallelization of the nearest-neighbor chain algorithm, and enables multiple clusters to be merged on every round. We introduce two key optimizations that are critical for efficiency: a range query optimization that reduces the number of distance computations required when finding nearest neighbors of clusters, and a caching optimization that stores a subset of previously computed distances, which are likely to be reused. Experimentally, we show that our highly-optimized implementations using 48 cores with two-way hyper-threading achieve 5.8--110.1x speedup over state-of-the-art parallel HAC algorithms and achieve 13.75--54.23x self-relative speedup. Compared to state-of-the-art algorithms, our algorithms require up to 237.3x less space. Our algorithms are able to scale to data set sizes with tens of millions of points, which existing algorithms are not able to handle.
翻译:本文研究等级分组问题, 其目标在于生成一个以不同尺度的数据集群集为代表群集的巢体。 我们提议 Par Chain 框架, 用于设计平行的等级群集群集( HAC) 算法, 并使用这个框架, 我们获得新的平行算法, 用于完整连接、 平均链接和沃德的连接标准。 与大多数先前的平行 HAC 算法相比, 我们的新算法只需要线性内存, 并且可以向大型数据集缩放。 Par Chain 是基于我们近邻连锁算法的平行化, 并且可以使每个回合的多个群组合并。 我们引入了两种关键优化, 这对于效率至关重要: 范围查询优化, 减少寻找最近的群集邻居、 平均链接和沃德的联系标准。 与大多数以前计算过的距离的一组算法相比, 这可能会被再利用。 实验性地, 我们用48个高精度核心实施, 双向超速读算算法, 实现5. 110.1x 速度速度, 我们的自动算算算算算算算算为13. 54 的自动算算算算算算算算算算算为更慢的自动算算算法, 。