Change Point Analysis of Multivariate Data via Multivariate Rank-based Distribution-free Nonparametric Testing Using Measure Transportation

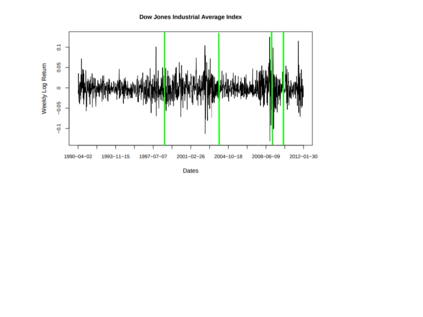
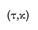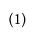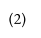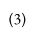In this paper, I propose a general algorithm for multiple change point analysis via multivariate distribution-free nonparametric testing based on the concept of ranks that are defined by measure transportation. Multivariate ranks and the usual one-dimensional ranks both share an important property: they are both distribution-free. This finding allows for the creation of nonparametric tests that are distribution-free under the null hypothesis. Here I will consider rank energy statistics in the context of the multiple change point problem. I will estimate the number of change points and each of their locations within a multivariate series of time-ordered observations. This paper will examine the multiple change point question in a broad setting in which the observed distributions and number of change points are unspecified, rather than assume the time series observations follow a parametric model or there is one change point, as many works in this area assume. The objective is to develop techniques for identifying change points while making as few presumptions as possible. This algorithm described here is based upon energy statistics and has the ability to detect any distributional change. Presented are the theoretical properties of this new algorithm and the conditions under which the approximate number of change points and their locations can be estimated. This newly proposed algorithm can be used to analyze various datasets, including financial and microarray data. This algorithm has also been successfully implemented in the R package recp, which is available on GitHub. A section of this paper is dedicated to the execution of this procedure, as well as the use of the recp package.