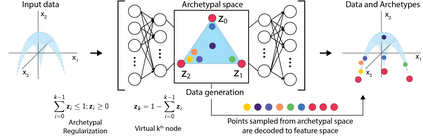
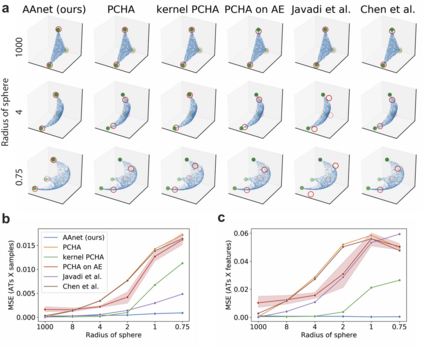
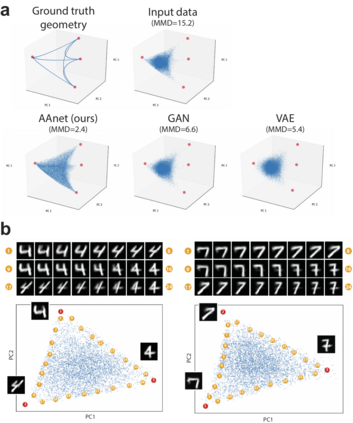
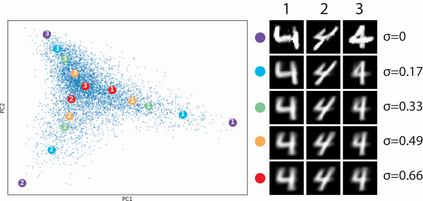
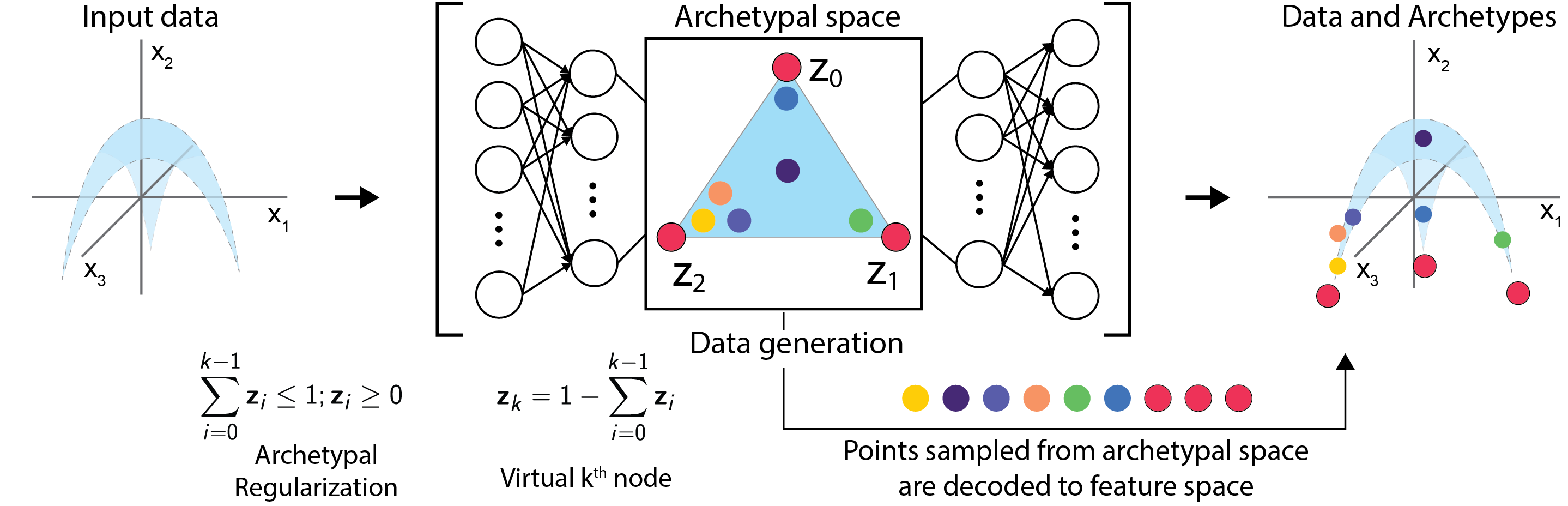
Archetypal analysis is a data decomposition method that describes each observation in a dataset as a convex combination of "pure types" or archetypes. These archetypes represent extrema of a data space in which there is a trade-off between features, such as in biology where different combinations of traits provide optimal fitness for different environments. Existing methods for archetypal analysis work well when a linear relationship exists between the feature space and the archetypal space. However, such methods are not applicable to systems where the feature space is generated non-linearly from the combination of archetypes, such as in biological systems or image transformations. Here, we propose a reformulation of the problem such that the goal is to learn a non-linear transformation of the data into a latent archetypal space. To solve this problem, we introduce Archetypal Analysis network (AAnet), which is a deep neural network framework for learning and generating from a latent archetypal representation of data. We demonstrate state-of-the-art recovery of ground-truth archetypes in non-linear data domains, show AAnet can generate from data geometry rather than from data density, and use AAnet to identify biologically meaningful archetypes in single-cell gene expression data.
翻译:箭头分析是一种数据分解方法,它将数据集中的每个观测描述为“纯类型”或成型的组合。这些成型类型代表了数据空间的极限,在其中各特征之间存在着权衡,例如在生物学中,不同特性的组合为不同环境提供了最佳的适应性。在地物空间和成型空间之间存在线性关系时,拱形分析的现有方法效果良好。然而,这些方法不适用于地物空间是来自成型组合的非线性生成的系统,例如生物系统或成型变异。我们在这里建议重新拟订问题,目的是学习数据的非线性转换为潜在的成一个潜在的成形体。为了解决这个问题,我们引入了拱形体分析网络(Anet),这是一个深层的神经网络框架,用于从潜在成型数据表示式中学习和生成。我们展示了从非直径直径型的成型直径直径直径直方形(从非直径直型)的直径直径直径直径直型(Anairnet)在非直径直径直型数据库中从非直径直径直径直径直型(A型)数据库型数据中生成数据生成数据生成数据,而不是直径直型(A-直型)数据库型数据显示,可以显示,从非直径直型号数据域数据域数据域数据域数据域中生成数据领域数据域中生成数据,从非正型号数据域域域域域域域域域域域中生成数据,显示数据域数据显示的恢复。