Random walk approximation for irreversible drift-diffusion process on manifold: ergodicity, unconditional stability and convergence

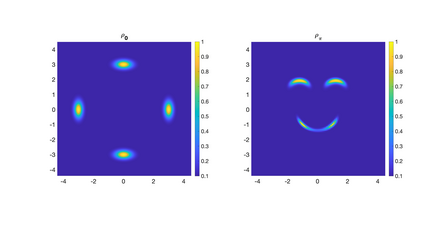
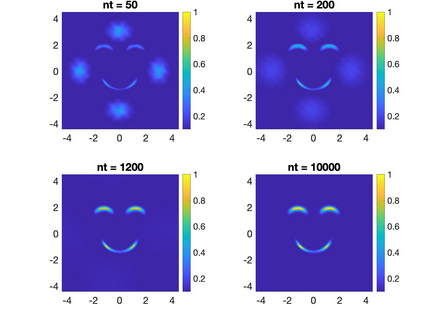
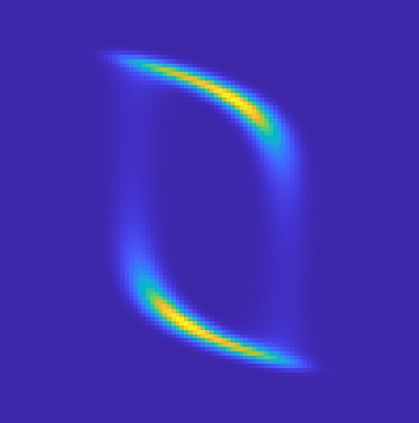
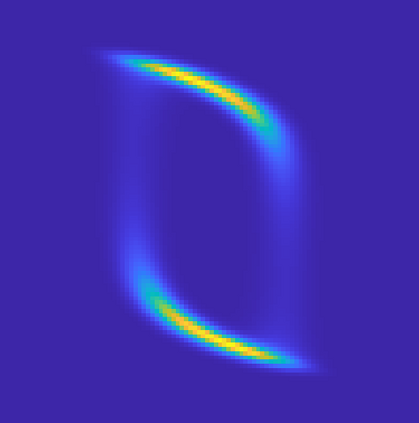
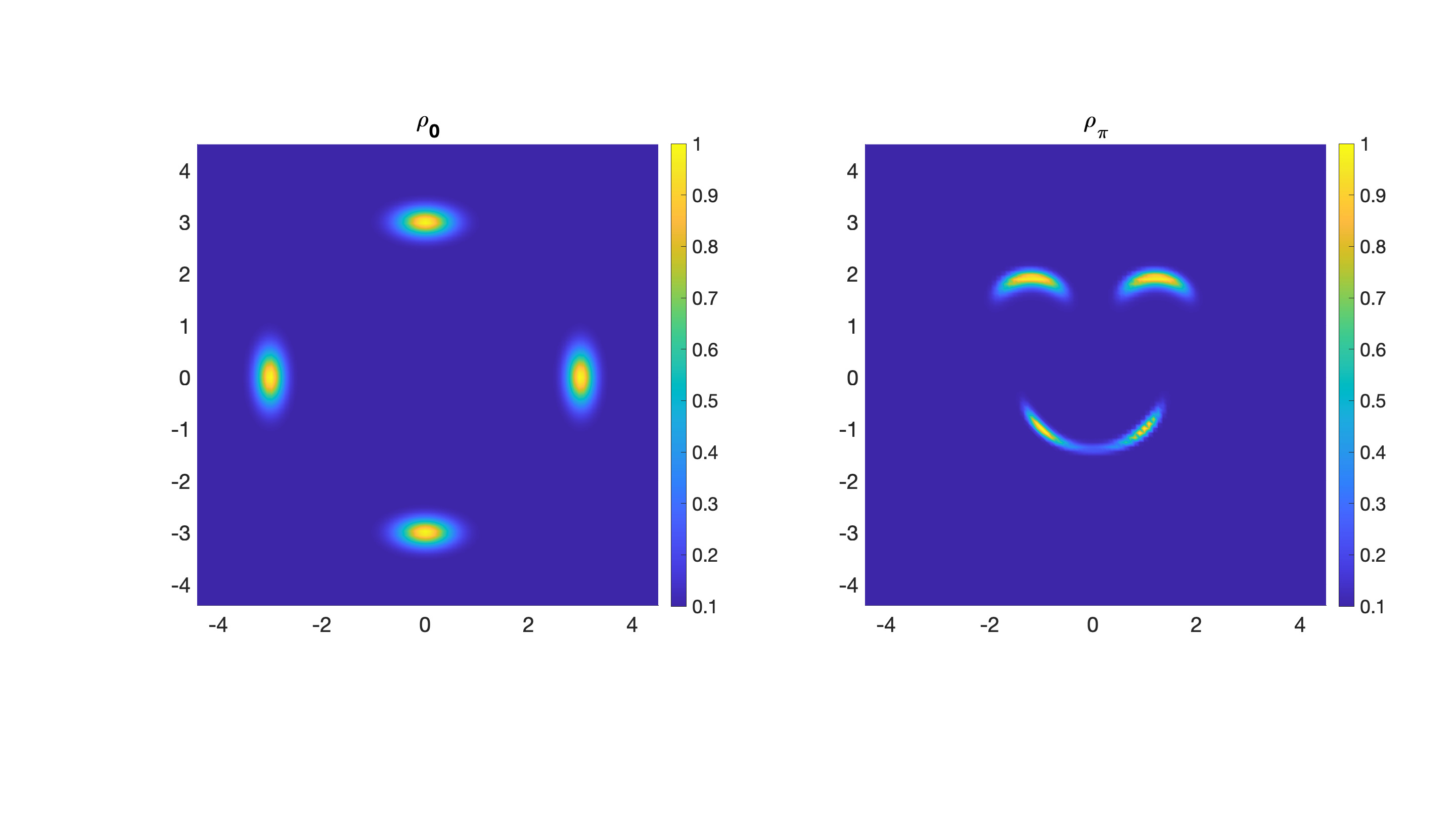
Irreversible drift-diffusion processes are very common in biochemical reactions. They have a non-equilibrium stationary state (invariant measure) which does not satisfy detailed balance. For the corresponding Fokker-Planck equation on a closed manifold, via Voronoi tessellation, we propose two upwind finite volume schemes with or without the information of the invariant measure. Both two schemes enjoy stochastic $Q$-matrix structures and can be decomposed as a gradient flow part and a Hamiltonian flow part, which enable us to prove unconditional stability, ergodicity and error estimates. Based on two upwind schemes, several numerical examples - including sampling accelerated by a mixture flow, image transformations and simulations for stochastic model of chaotic system - are conducted. These two structure-preserving schemes also give a natural random walk approximation for a generic irreversible drift-diffusion process on a manifold. Thus they can be adapted to manifold-related computations induced from high dimensional molecular dynamics.