A convergent finite element algorithm for mean curvature flow in higher codimension

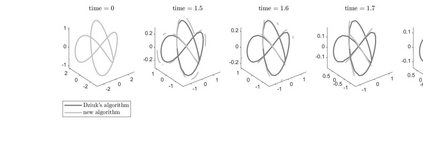
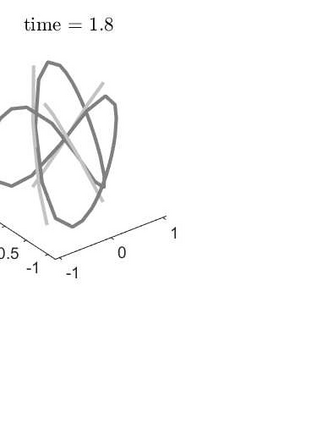
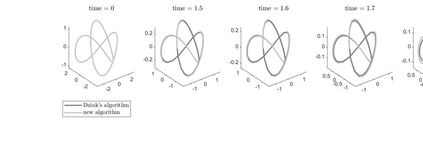
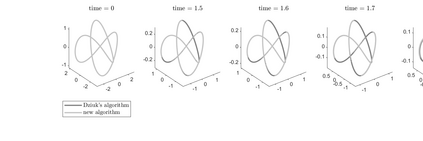
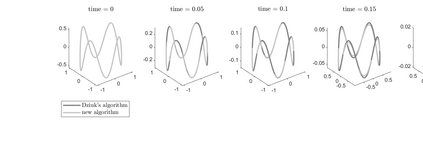
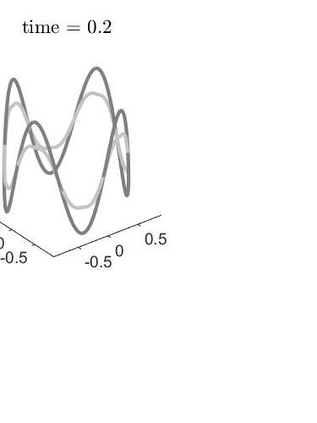
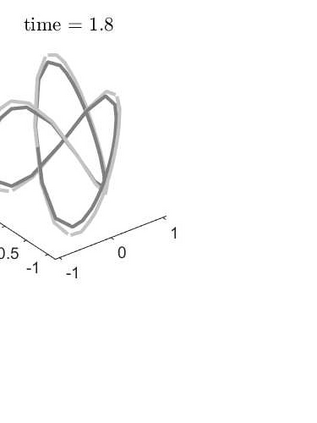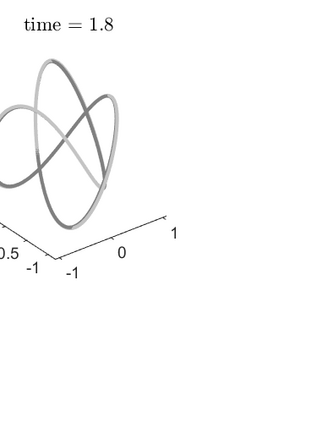Optimal-order uniform-in-time $H^1$-norm error estimates are given for semi- and full discretizations of mean curvature flow of surfaces in arbitrarily high codimension. The proposed and studied numerical method is based on a parabolic system coupling the surface flow to evolution equations for the mean curvature vector and for the orthogonal projection onto the tangent space. The algorithm uses evolving surface finite elements and linearly implicit backward difference formulae. This numerical method admits a convergence analysis in the case of finite elements of polynomial degree at least two and backward difference formulae of orders two to five. Numerical experiments in codimension 2 illustrate and complement our theoretical results.