Age of information without service preemption

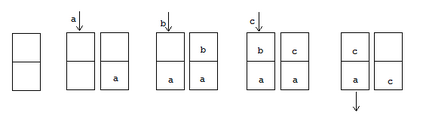
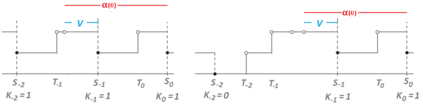
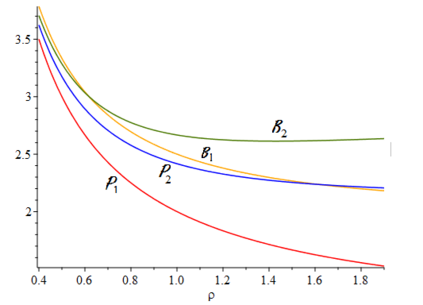
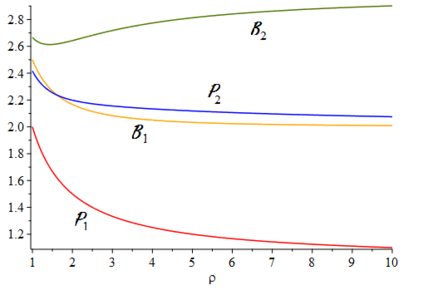
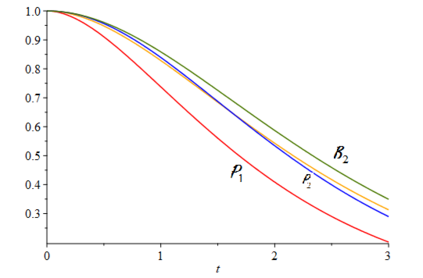
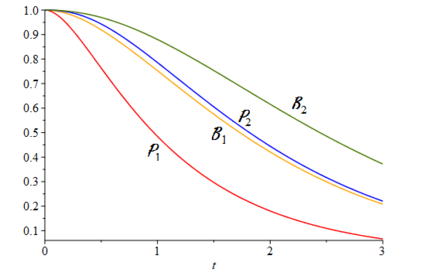
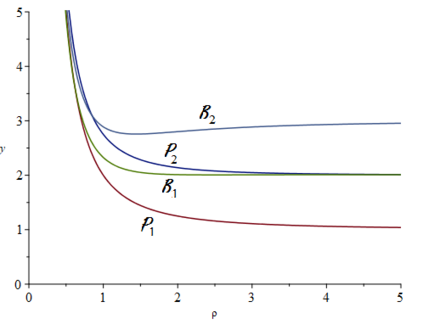
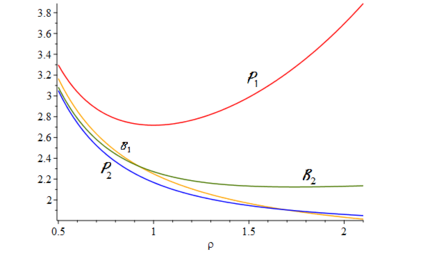
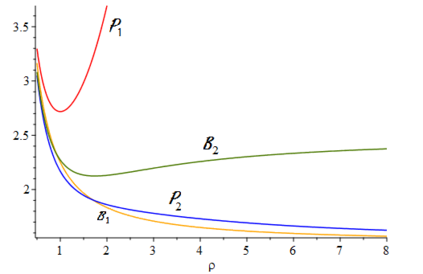
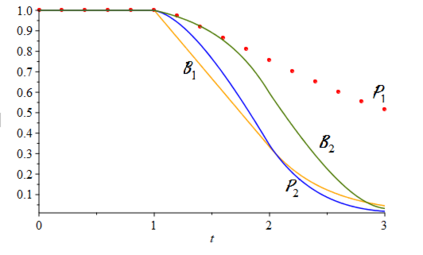
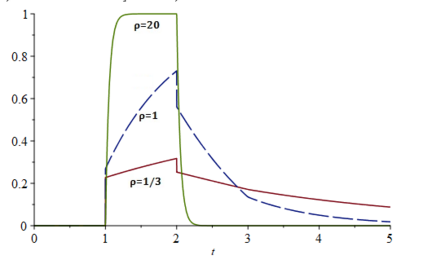
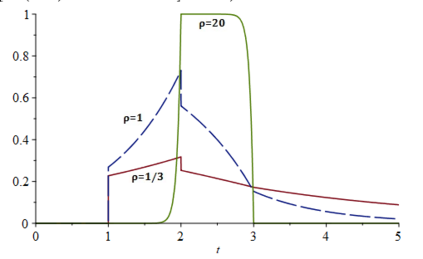
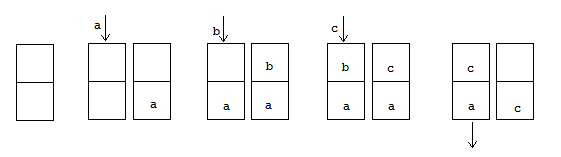
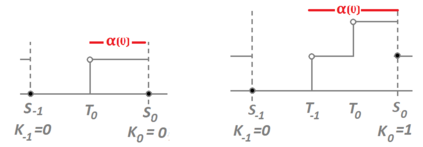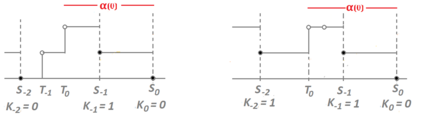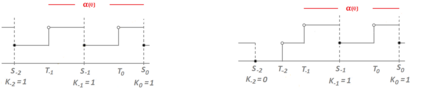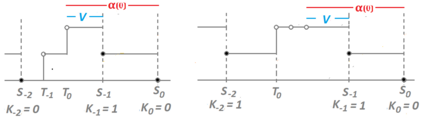When designing a message transmission system, from the point of view of making sure that the information transmitted is as fresh as possible, two rules of thumb seem reasonable: use small buffers and adopt a last-in-first-out policy. In this paper, we measure freshness of information using the recently adopted "age of information" performance measure. Considering it as a stochastic process operating in a stationary regime, we compute not just the first moment but the whole marginal distribution of the age of information (something important in applications) for two well-performing systems. In neither case do we allow for preemption of the message being processed because this may be difficult to implement in practice. We assume that the arrival process is Poisson and that the messages have independent sizes (service times) with common distribution. We use Palm and Markov-renewal theory to derive explicit results for Laplace transforms which, in many cases can be inverted analytically. We discuss how well the systems we analyze performs and examine how close to optimality they are. In particular, we answer an open question that was raised in [9] regarding the optimality of the system denoted as P2.