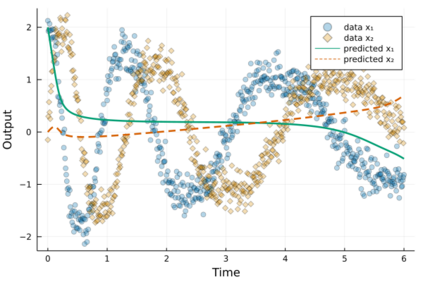
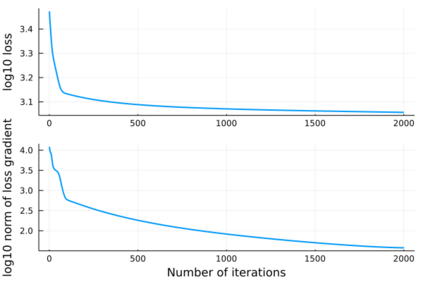
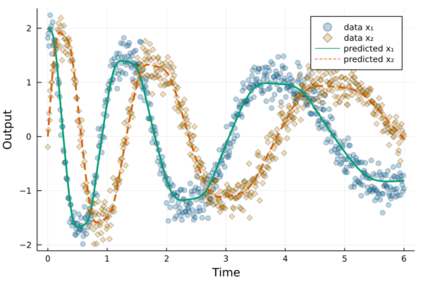
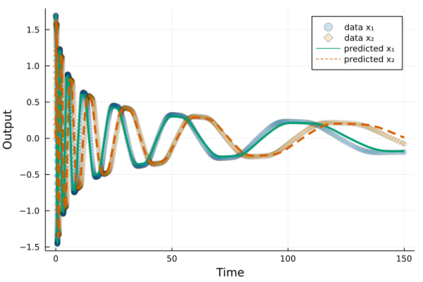
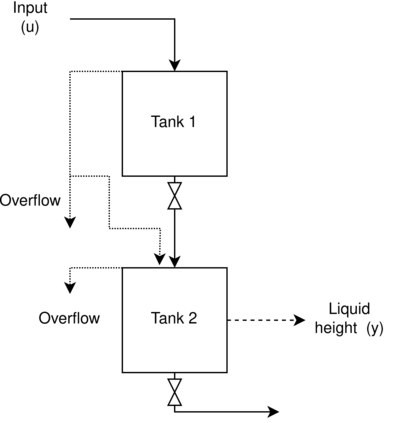
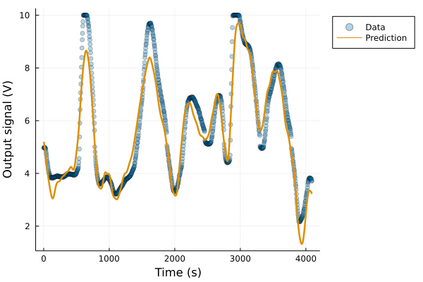
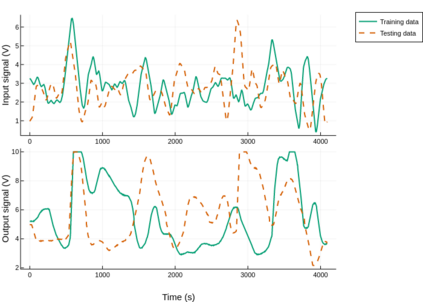
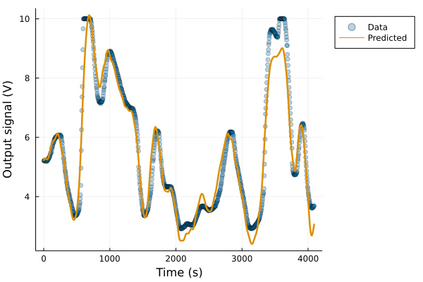
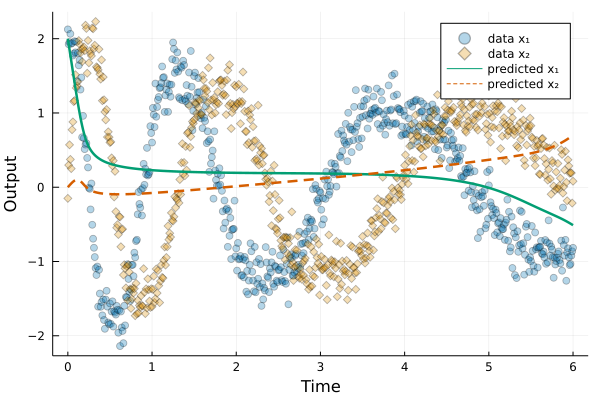
Neural differential equations have recently emerged as a flexible data-driven/hybrid approach to model time-series data. This work experimentally demonstrates that if the data contains oscillations, then standard fitting of a neural differential equation may give flattened out trajectory that fails to describe the data. We then introduce the multiple shooting method and present successful demonstrations of this method for the fitting of a neural differential equation to two datasets (synthetic and experimental) that the standard approach fails to fit. Constraints introduced by multiple shooting can be satisfied using a penalty or augmented Lagrangian method.
翻译:最近出现了神经差异方程式,作为数据驱动/混合的灵活方法来模拟时间序列数据,这项工作实验性地证明,如果数据含有振动,那么神经差异方程式的标准安装可能会使没有描述数据的轨迹平坦下来。然后我们引入多种射击方法,并成功演示这一方法,将神经差异方程式与标准方法不合适的两个数据集(合成和实验)相匹配。如果使用惩罚或强化拉格朗江方法,可以满足多次射击带来的限制。