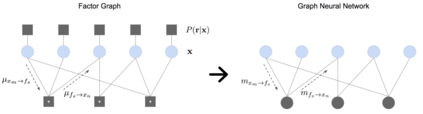
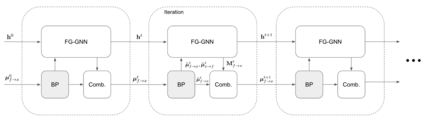
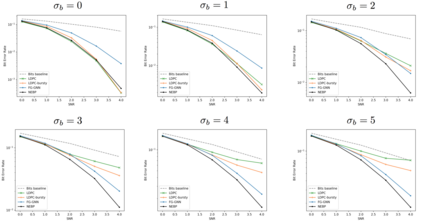
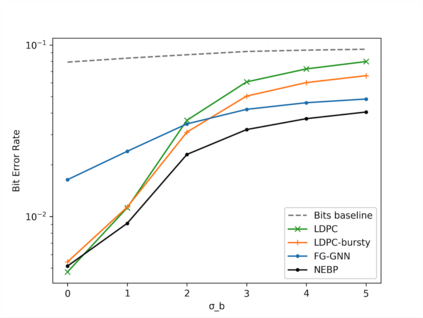
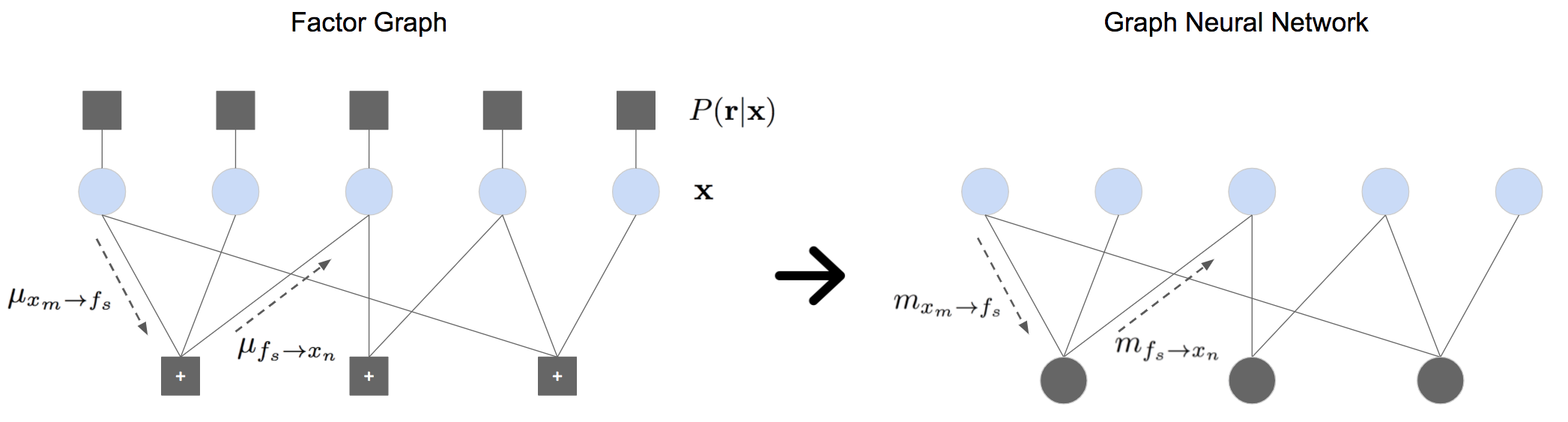
A graphical model is a structured representation of locally dependent random variables. A traditional method to reason over these random variables is to perform inference using belief propagation. When provided with the true data generating process, belief propagation can infer the optimal posterior probability estimates in tree structured factor graphs. However, in many cases we may only have access to a poor approximation of the data generating process, or we may face loops in the factor graph, leading to suboptimal estimates. In this work we first extend graph neural networks to factor graphs (FG-GNN). We then propose a new hybrid model that runs conjointly a FG-GNN with belief propagation. The FG-GNN receives as input messages from belief propagation at every inference iteration and outputs a corrected version of them. As a result, we obtain a more accurate algorithm that combines the benefits of both belief propagation and graph neural networks. We apply our ideas to error correction decoding tasks, and we show that our algorithm can outperform belief propagation for LDPC codes on bursty channels.
翻译:图形模型是一个基于本地的随机变量的结构化表示。 这些随机变量的一种传统解释方法是使用信仰传播来进行推断。 当提供真实的数据生成过程时, 信仰传播可以推断树形结构要素图中的最佳远地点概率估计。 但是, 在许多情况下, 我们可能只能访问数据生成过程的差近近, 或者我们可能会在系数图中面临循环, 导致亚最佳估计。 在此工作中, 我们首先将图形神经网络扩展为元素图( FG- GNN) 。 我们然后提议一个新的混合模型, 与信仰传播同时运行 FG- GNN 。 FG- GNN 接收来自每个推断的信念传播的信息, 并输出一个正确的版本。 结果, 我们获得一个更准确的算法, 将信仰传播和图形神经网络的效益结合起来。 我们应用我们的想法来校正错误解码任务, 我们的算法可以超越对防爆通道的 LDPC 代码的信念传播。