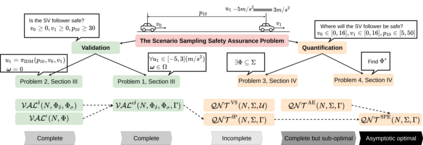
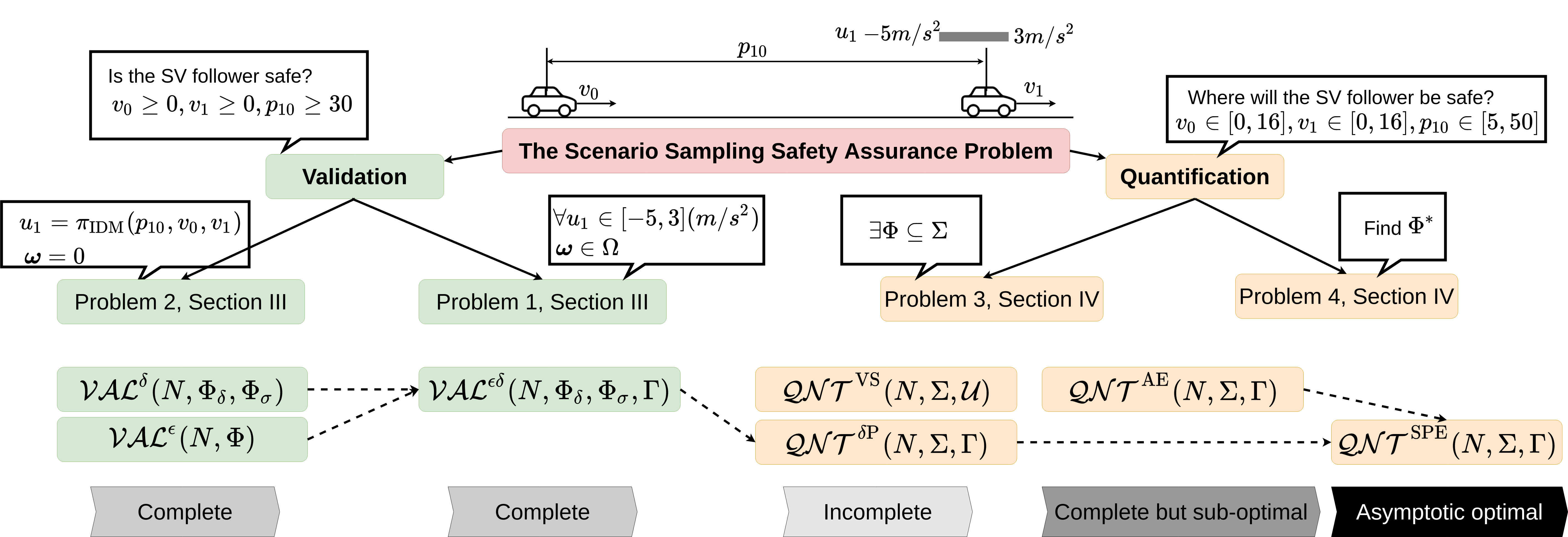
How many scenarios are sufficient to validate the safe Operational Design Domain (ODD) of an Automated Driving System (ADS) equipped vehicle? Is a more significant number of sampled scenarios guaranteeing a more accurate safety assessment of the ADS? Despite the various empirical success of ADS safety evaluation with scenario sampling in practice, some of the fundamental properties are largely unknown. This paper seeks to remedy this gap by formulating and tackling the scenario sampling safety assurance problem from a set invariance perspective. First, a novel conceptual equivalence is drawn between the scenario sampling safety assurance problem and the data-driven robustly controlled forward invariant set validation and quantification problem. This paper then provides a series of resolution complete and probabilistic complete solutions with finite-sampling analyses for the safety validation problem that authenticates a given ODD. On the other hand, the quantification problem escalates the validation challenge and starts looking for a safe sub-domain of a particular property. This inspires various algorithms that are provably probabilistic incomplete, probabilistic complete but sub-optimal, and asymptotically optimal. Finally, the proposed asymptotically optimal scenario sampling safety quantification algorithm is also empirically demonstrated through simulation experiments.
翻译:有多少设想方案足以证明自动驾驶系统装备的车辆的安全操作设计域(ODD) 的安全操作设计域(ODD)? 是否有数量更多的抽样假设方案保证对ADS进行更准确的安全评估? 尽管ADS安全评价在实际中通过情景抽样取得了各种成功经验,但有些基本特性基本上还不清楚。本文件力求从一套变量的角度制定和解决假设方案抽样安全保障问题,以此弥补这一差距。首先,在假设方案抽样安全保证问题与数据驱动的动态强控的变异定置验证和量化问题之间得出了一种新的概念等同。本文随后提供了一系列完整和概率完整的解决方案,对安全验证问题进行了有限的抽样分析,以验证给给某个ODD作认证。另一方面,量化问题使验证挑战升级,并开始寻找特定属性的安全次域。这激发了各种可以肯定的概率性算法,即抽样保证问题完整而次优劣性,并尽可能优化。最后,拟议的模拟模型分析也是通过模拟性最佳的模型分析法。