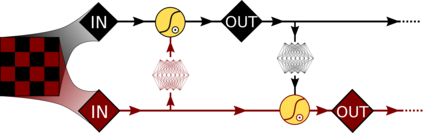
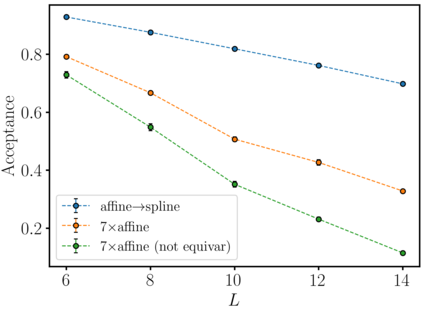
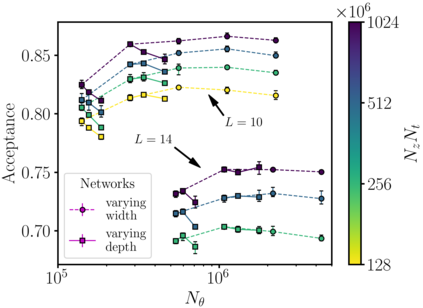
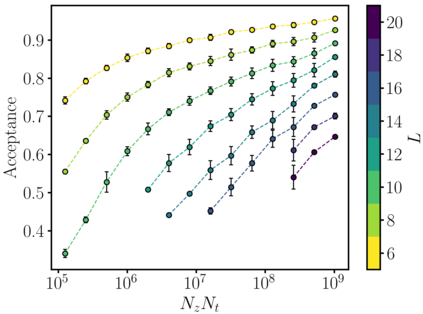
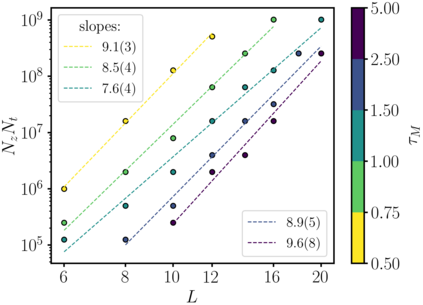
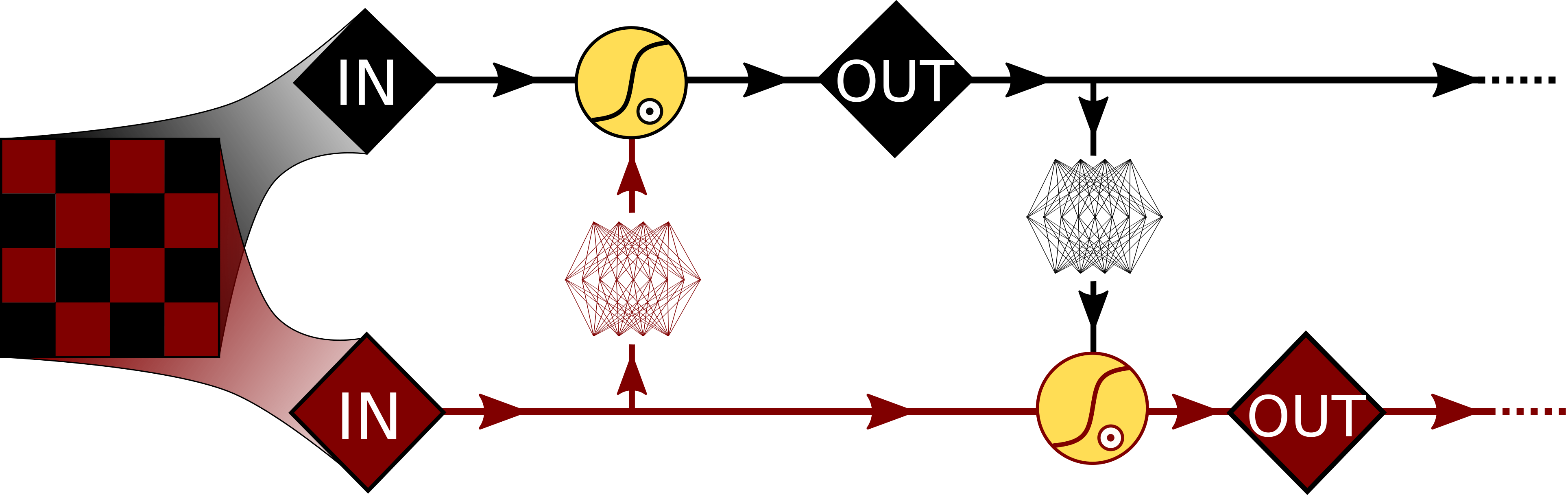
A trivializing map is a field transformation whose Jacobian determinant exactly cancels the interaction terms in the action, providing a representation of the theory in terms of a deterministic transformation of a distribution from which sampling is trivial. Recently, a proof-of-principle study by Albergo, Kanwar and Shanahan [arXiv:1904.12072] demonstrated that approximations of trivializing maps can be `machine-learned' by a class of invertible, differentiable neural models called \textit{normalizing flows}. By ensuring that the Jacobian determinant can be computed efficiently, asymptotically exact sampling from the theory of interest can be performed by drawing samples from a simple distribution and passing them through the network. From a theoretical perspective, this approach has the potential to become more efficient than traditional Markov Chain Monte Carlo sampling techniques, where autocorrelations severely diminish the sampling efficiency as one approaches the continuum limit. A major caveat is that it is not yet understood how the size of models and the cost of training them is expected to scale. As a first step, we have conducted an exploratory scaling study using two-dimensional $\phi^4$ with up to $20^2$ lattice sites. Although the scope of our study is limited to a particular model architecture and training algorithm, initial results paint an interesting picture in which training costs grow very quickly indeed. We describe a candidate explanation for the poor scaling, and outline our intentions to clarify the situation in future work.
翻译:一个微不足道的地图是一个实地变迁,其叶柯比决定因素完全取消了行动中的互动术语,它代表了理论的理论,它代表了对分布分布进行决定性转变的理论,而抽样则微不足道。最近,Albergo、Kanwar和Shanahan[arXiv:1904.12072]进行的一项原则证明研究表明,对图进行简单化的地图[arXiv:1904.12072]的证明性研究表明,通过一个称为“Textit(正常流)”的一类不可逆、可区别的神经模型,可以“机械化地获取”地图的近似近似值“机械化”。通过确保能够高效率地计算出雅各布决定因素,从利益理论中进行非现性精确的抽样,可以通过从简单的分布中抽取样本并通过网络传递这些样本。从理论上看,这一方法有可能比传统的Markov链 Monte Carlo取样技术更有效,其中的自动化关系会严重降低取样效率,因为一个叫“机械化”的模型的规模和训练费用预期会如何扩大。作为第一步,我们用二维的模型进行探索性规模研究,我们最初的模型的模型进行一个有限的研究,其规模到将来的模型,我们的研究范围是20xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx