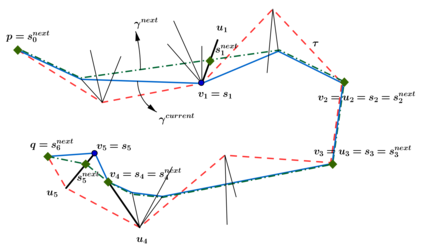
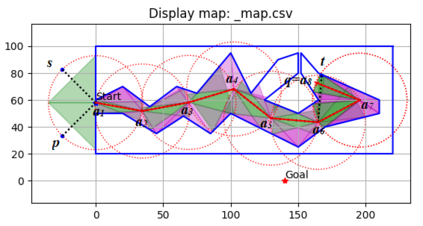
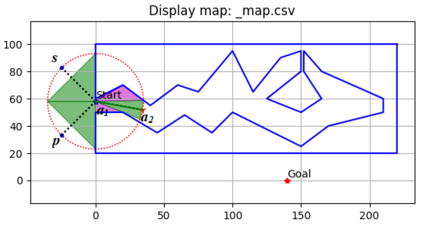
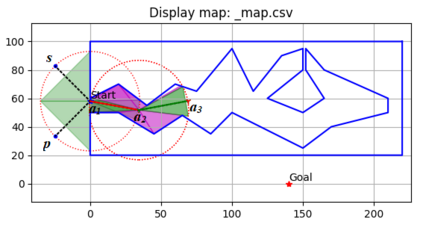
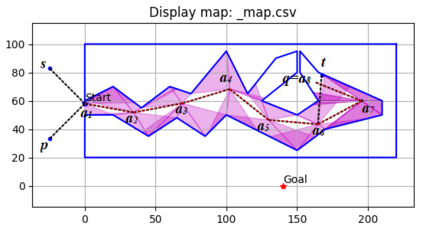
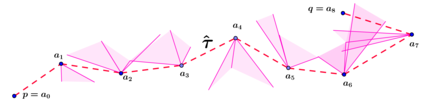
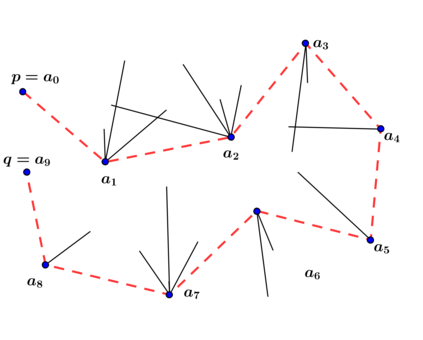
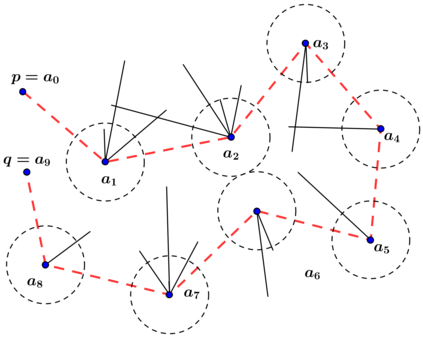
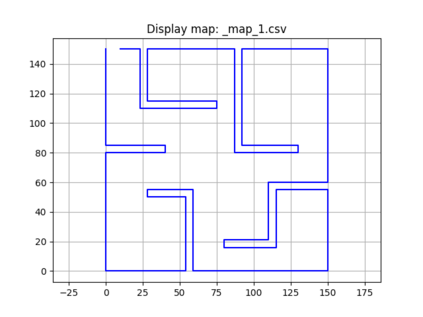
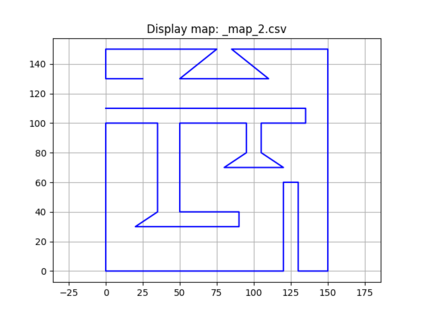
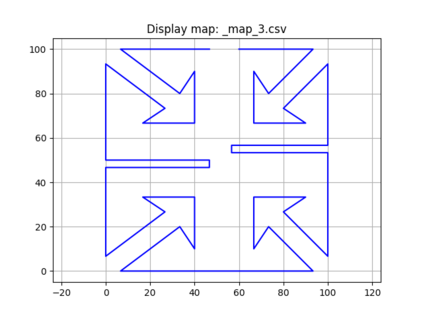
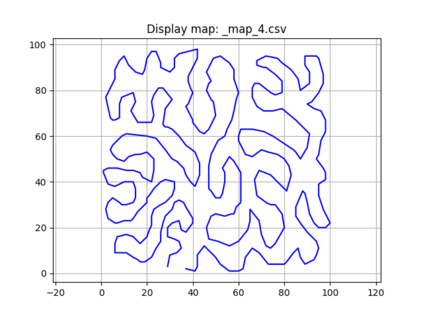
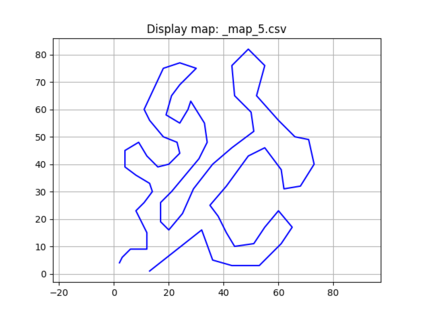
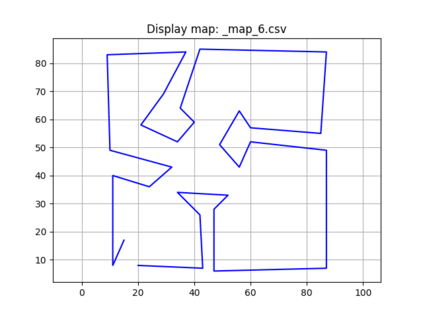
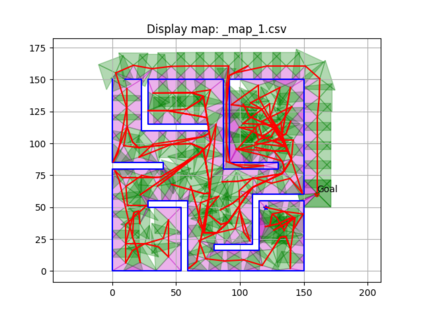
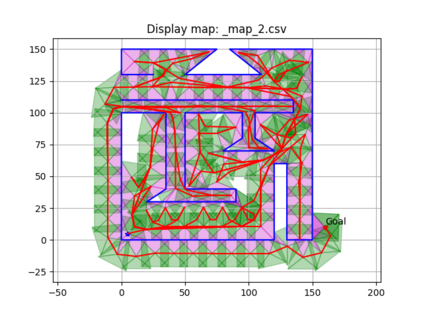
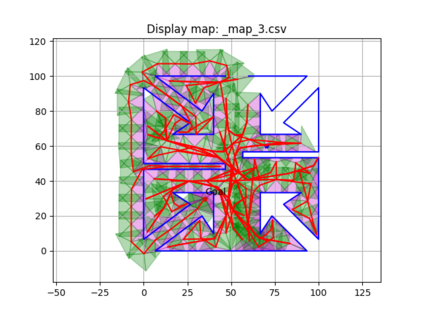
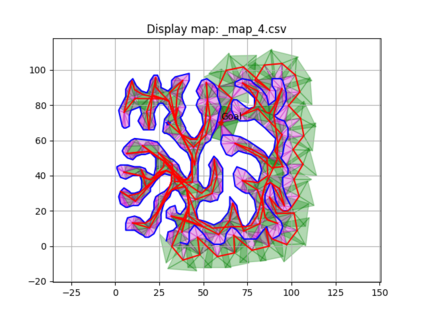
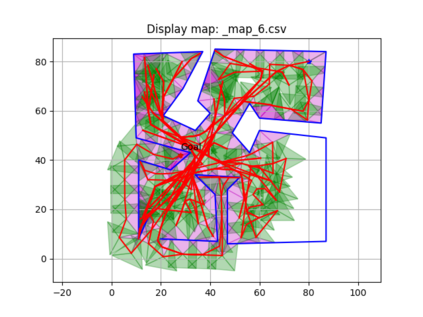
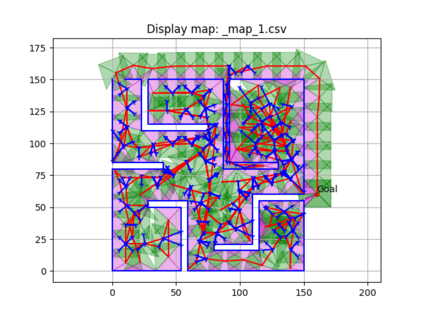
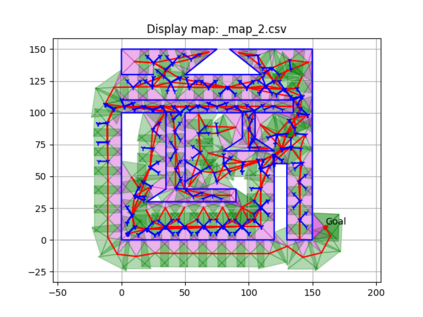
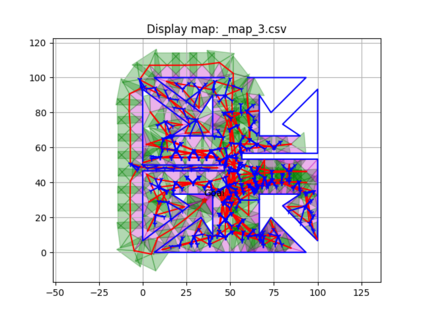
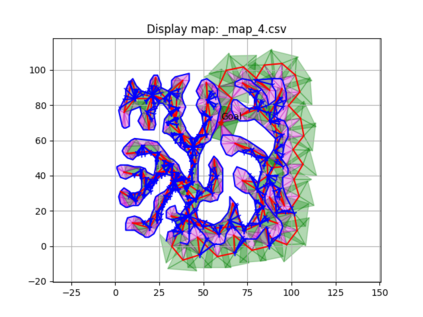
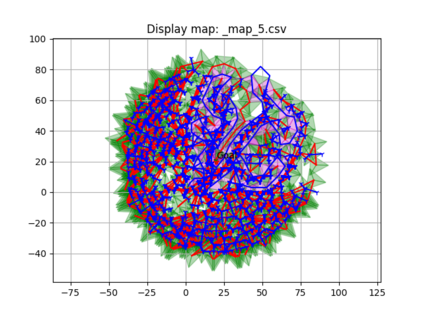
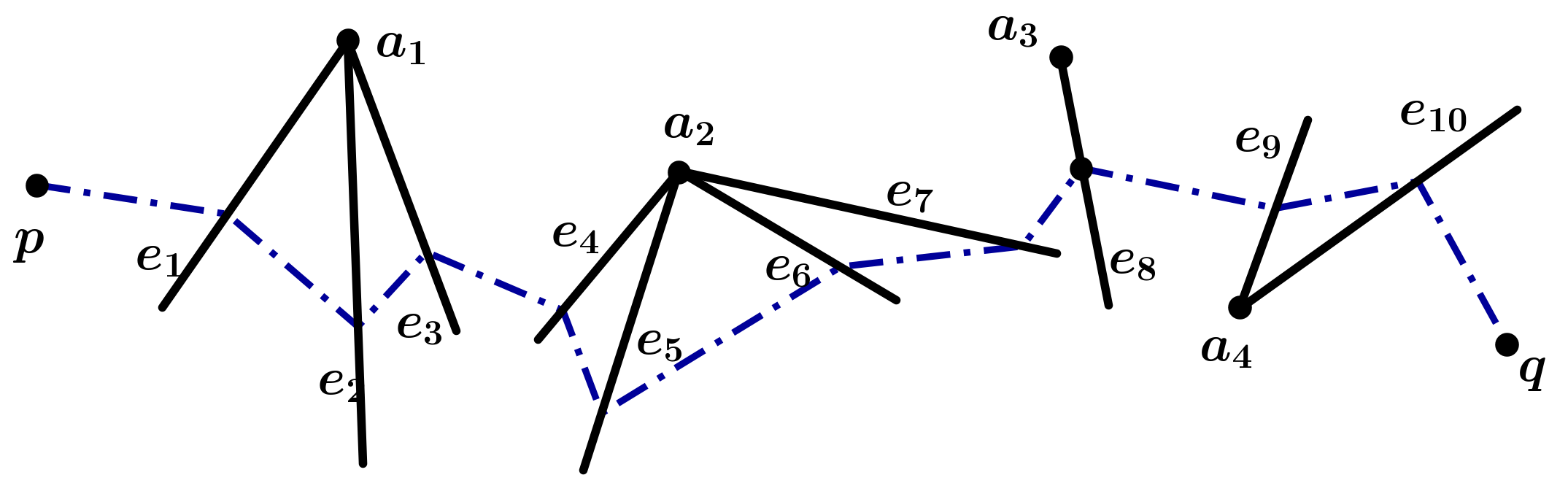
An autonomous robot with a limited vision range finds a path to the goal in an unknown environment in 2D avoiding polygonal obstacles. In the process of discovering the environmental map, the robot has to return to some positions marked previously, the regions where the robot traverses to return are defined as sequences of bundles of line segments. This paper presents a novel algorithm for finding approximately shortest paths along the sequences of bundles of line segments based on the method of multiple shooting. Three factors of the approach including bundle partition, collinear condition, and update of shooting points are presented. We then show that if the collinear condition holds, the exactly shortest paths of the problems are determined, otherwise, the sequence of paths obtained by the update of the method converges to the shortest path. The algorithm is implemented in Python and some numerical examples show that the running time of path-planning for autonomous robots using our method is faster than that using the rubber band technique of Li and Klette in Euclidean Shortest Paths, Springer, 53-89 (2011).
翻译:视野范围有限的自主机器人在2D避免多边形障碍的未知环境中找到目标路径。 在发现环境地图的过程中, 机器人必须返回以前标记的一些位置, 返回的机器人跨行区域被定义为线段捆绑的序列。 本文展示了一种根据多发射击方法在线段捆绑序列中找到近乎最短路径的新型算法。 展示了三种方法要素, 包括捆绑分割、 共线性条件和射击点更新。 我们然后显示, 如果保线条件保持, 问题的确切最短路径会被确定为最短路径, 否则, 通过更新方法获得的路径序列会与最短路径一致。 算法在Python实施, 一些数字实例显示, 使用我们的方法对自主机器人进行路径规划的运行时间比使用Euclidean最短路径的Li和Klette的橡皮带技术、 Springer、 53- 89 (2011年) 的运行速度要快。