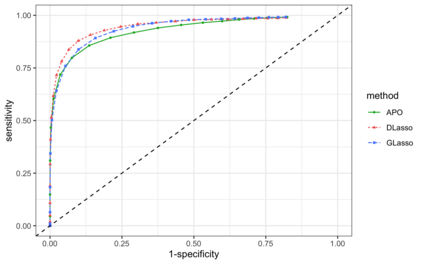
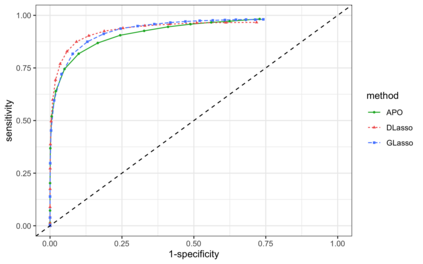
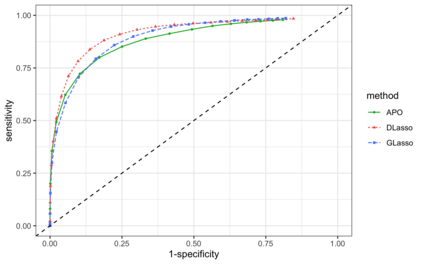
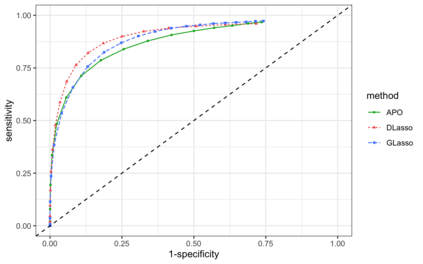
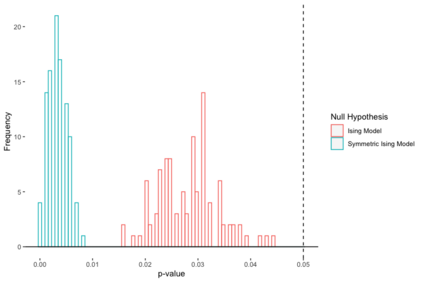
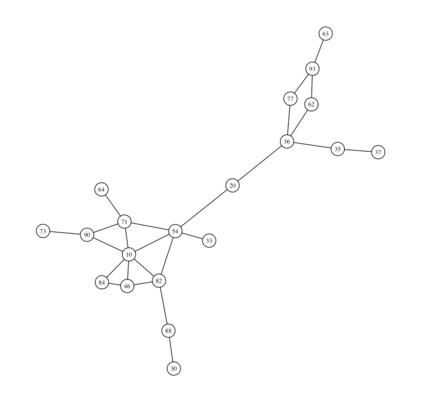
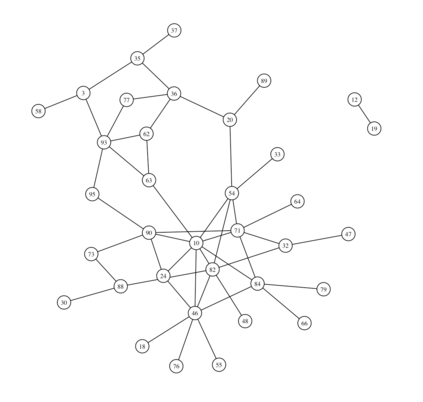
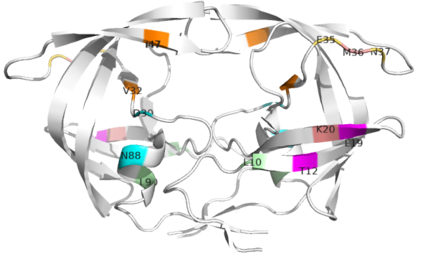
We introduce a nonparametric graphical model for discrete node variables based on additive conditional independence. Additive conditional independence is a three way statistical relation that shares similar properties with conditional independence by satisfying the semi-graphoid axioms. Based on this relation we build an additive graphical model for discrete variables that does not suffer from the restriction of a parametric model such as the Ising model. We develop an estimator of the new graphical model via the penalized estimation of the discrete version of the additive precision operator and establish the consistency of the estimator under the ultrahigh-dimensional setting. Along with these methodological developments, we also exploit the properties of discrete random variables to uncover a deeper relation between additive conditional independence and conditional independence than previously known. The new graphical model reduces to a conditional independence graphical model under certain sparsity conditions. We conduct simulation experiments and analysis of an HIV antiretroviral therapy data set to compare the new method with existing ones.
翻译:我们引入了基于添加性条件独立的离散节点变量的非参数图形模型。 添加性有条件独立是一种三种方式的统计关系,它通过满足半成像轴承,以有条件独立的方式共享类似属性。 基于此关系,我们为不受到Ising模型等参数模型限制的离散变量构建了一个添加性图形模型。我们通过对添加性精度操作器离散版本进行适度估计,为新的图形模型开发一个估计符,并在超高维环境下建立测算器的一致性。除了这些方法的发展外,我们还利用离散随机变量的特性,以发现比以前已知的更深的添加性有条件独立和有条件独立之间的关系。新的图形模型在某些宽度条件下将条件性减为有条件的独立图形模型。我们进行模拟实验和分析艾滋病毒抗逆转录病毒疗法数据集,以将新方法与现有方法进行比较。