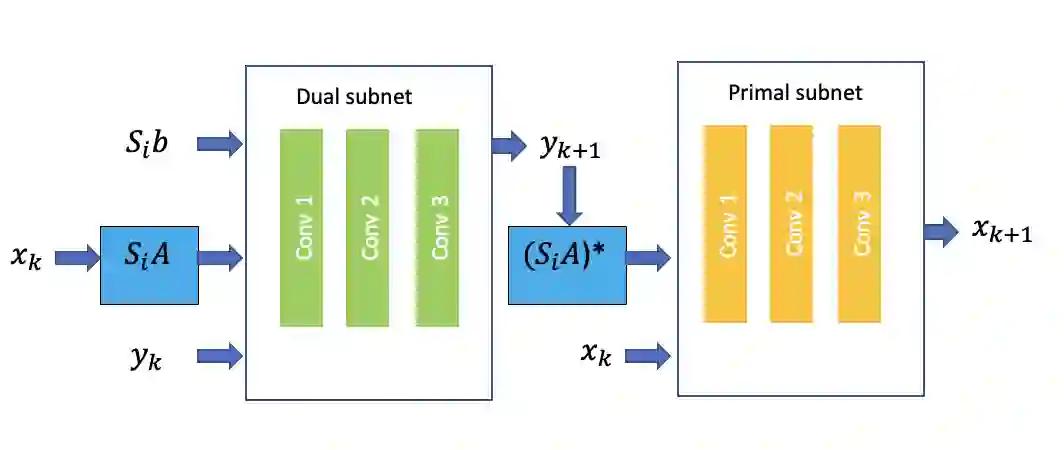
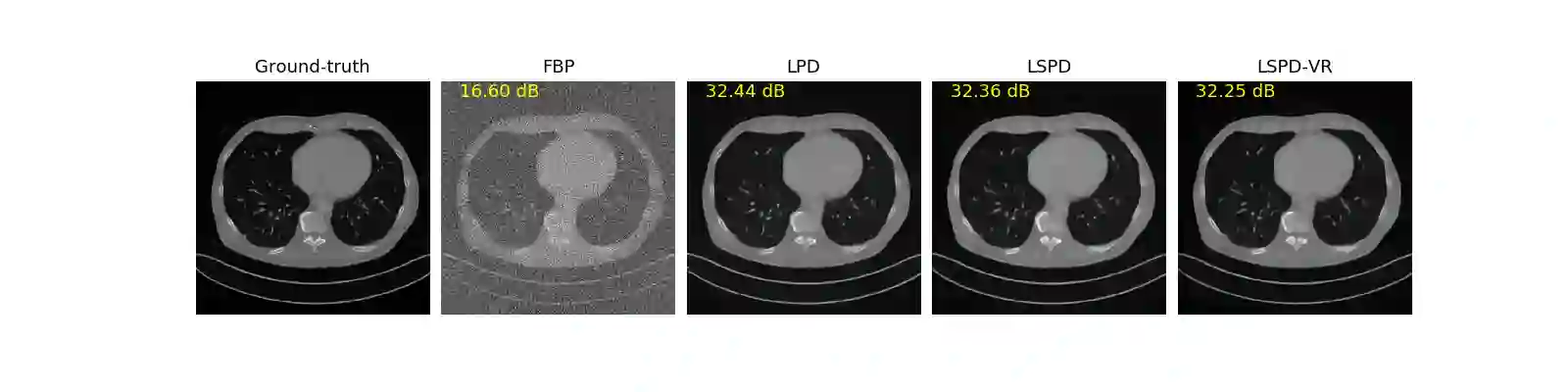
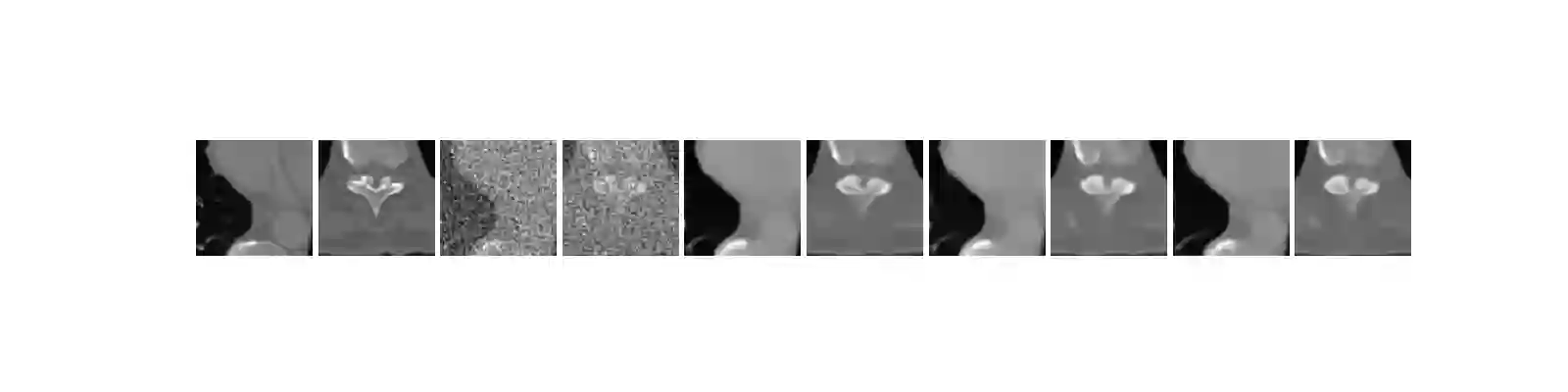
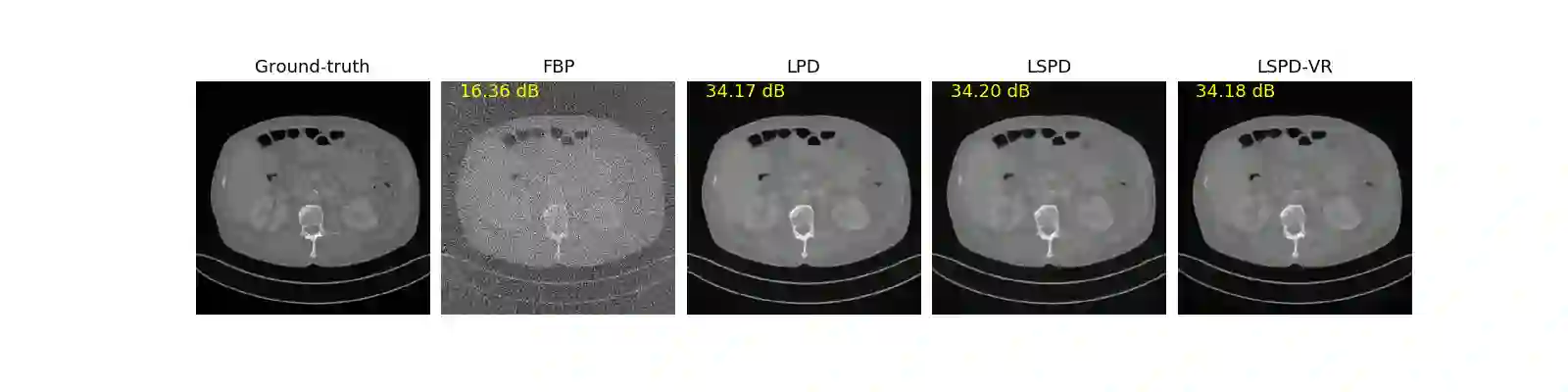
We propose a new type of efficient deep-unrolling networks for solving imaging inverse problems. Conventional deep-unrolling methods require full forward operator and its adjoint across each layer, and hence can be significantly more expensive computationally as compared with other end-to-end methods that are based on post-processing of model-based reconstructions, especially for 3D image reconstruction tasks. We develop a stochastic (ordered-subsets) variant of the classical learned primal-dual (LPD), which is a state-of-the-art unrolling network for tomographic image reconstruction. The proposed learned stochastic primal-dual (LSPD) network only uses subsets of the forward and adjoint operators and offers considerable computational efficiency. We provide theoretical analysis of a special case of our LSPD framework, suggesting that it has the potential to achieve image reconstruction quality competitive with the full-batch LPD while requiring only a fraction of the computation. The numerical results for two different X-ray computed tomography (CT) imaging tasks (namely, low-dose and sparse-view CT) corroborate this theoretical finding, demonstrating the promise of LSPD networks for large-scale imaging problems.
翻译:我们提出了一种新型高效的深层滚动网络,以解决成像反面问题。常规的深层滚动方法需要全前端操作员及其各层之间的连接,因此,与基于模型重建的后处理,特别是3D图像重建任务的其他端对端方法相比,计算成本可能大大高于其他端对端方法。我们开发了古典学识丰富的原始面图(LPD)的随机(有秩序子集)变体(有秩序的子集)变体,这是用于重建成像图像的最先进的解动网络。提议的深层原始面图(LSPD)网络仅使用前端和联合操作员的子集体,提供相当的计算效率。我们从理论上分析了我们的LSPD框架的一个特例,表明它有可能与全尺寸LPD(全尺寸LPD)相比实现图像重建质量竞争,但只需要一小部分计算。两个不同的X光光图成像(CT)成像任务(即低剂量和低视力成像网络)的数字结果证实了这一理论性发现,展示了大比例成像系统问题的前景。