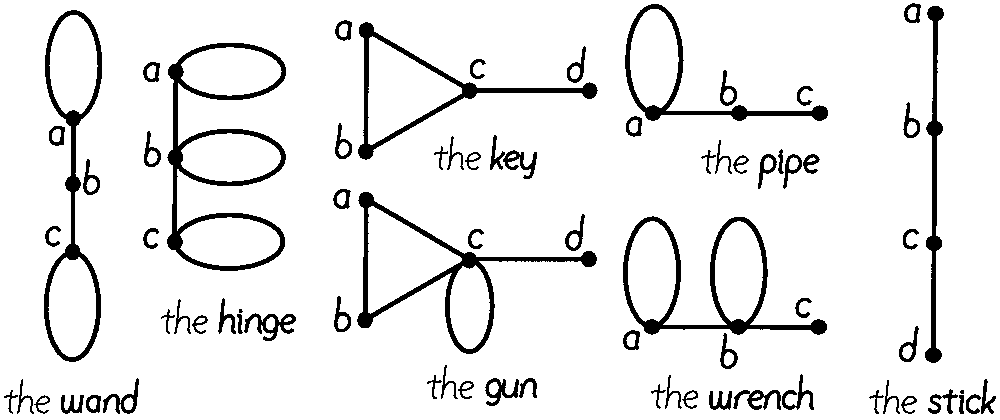
We study the problem of counting the number of homomorphisms from an input graph $G$ to a fixed (quantum) graph $\bar{H}$ in any finite field of prime order $\mathbb{Z}_p$. The subproblem with graph $H$ was introduced by Faben and Jerrum [ToC'15] and its complexity is subject to a growing series of research articles, e.g. the work of Focke, Goldberg, Roth, and Zivn\'y [SIDMA'21] and the work of Bulatov and Kazeminia [STOC'22], subsequent to this article's conference version. Our contribution is threefold. First, we introduce the study of quantum graphs to the study of modular counting homomorphisms. We show that the complexity for a quantum graph $\bar{H}$ collapses to the complexity criteria found at dimension 1: graphs. Second, in order to prove cases of intractability we establish a further reduction to the study of bipartite graphs. Lastly, we establish a dichotomy for all bipartite ($K_{3,3}\backslash\{e\}$, ${domino}$)-free graphs by a thorough structural study incorporating both local and global arguments. This result subsumes all results on bipartite graphs known for all prime moduli and extends them significantly. Even for the subproblem with $p$ equal to $2$, this establishes new results.
翻译:我们研究了从一个输入图形$G$到一个固定(quantum)图形$\bar{H} $\bar{H}$(mathb ⁇ p$) 等值计算同质体数量的问题。 由Faben 和 Jerrum [ToC'15] 提出, 其复杂性取决于越来越多的一系列研究文章, 例如Focke、 Goldberg、 Roth 和 Zivn\'y [SIDMA'21] 的工作, 以及Bulatov 和Kazeminia [STOC'22] 的工作, 这篇文章的会议版本之后。 我们的贡献是三重。 首先, 我们介绍量数图的子问题, $bar{H} 和它的复杂程度都取决于第1维度的复杂标准。 第二, 为了证明对双面图的研究的吸引力, 我们为所有双面图的平面图结果($$_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________