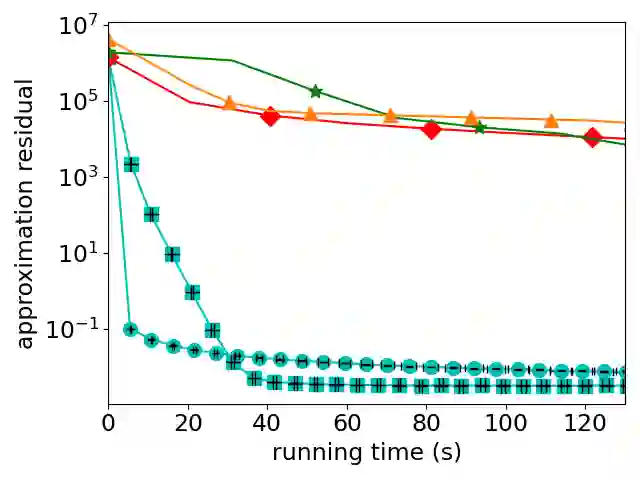
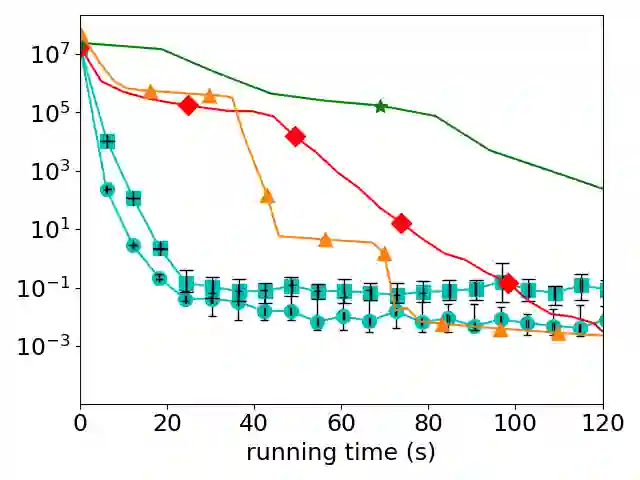
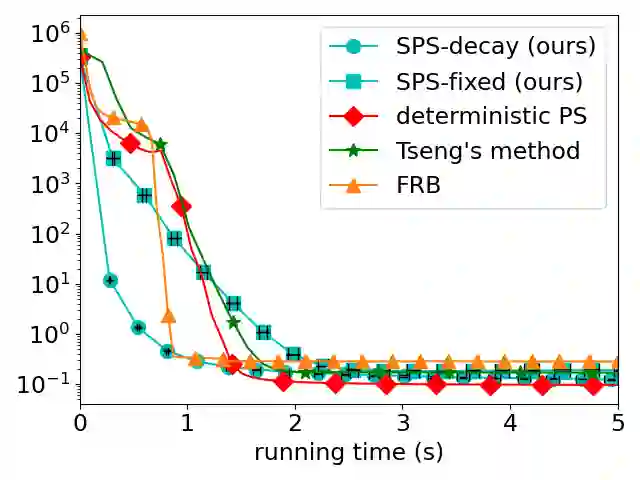
We present a new, stochastic variant of the projective splitting (PS) family of algorithms for monotone inclusion problems. It can solve min-max and noncooperative game formulations arising in applications such as robust ML without the convergence issues associated with gradient descent-ascent, the current de facto standard approach in such situations. Our proposal is the first version of PS able to use stochastic (as opposed to deterministic) gradient oracles. It is also the first stochastic method that can solve min-max games while easily handling multiple constraints and nonsmooth regularizers via projection and proximal operators. We close with numerical experiments on a distributionally robust sparse logistic regression problem.
翻译:我们提出了一个新的、随机变体,用于预测分解(PS)的算法组合,用于处理单调包容问题,它可以解决在稳健的 ML等应用中产生的微量和不合作的游戏配方,而没有与梯度下降率相关的趋同问题,即目前这种情况下的实际标准做法。我们的提案是能够使用静态(相对于确定性)梯度或触角的PS的第一版。它也是第一个能够解决微量成交游戏的随机方法,同时通过投影和准氧化操作者很容易地处理多种限制和非吸附式的调节器。我们结束关于分布性强、稀少的物流回归问题的数字实验。