The Exact Class of Graph Functions Generated by Graph Neural Networks

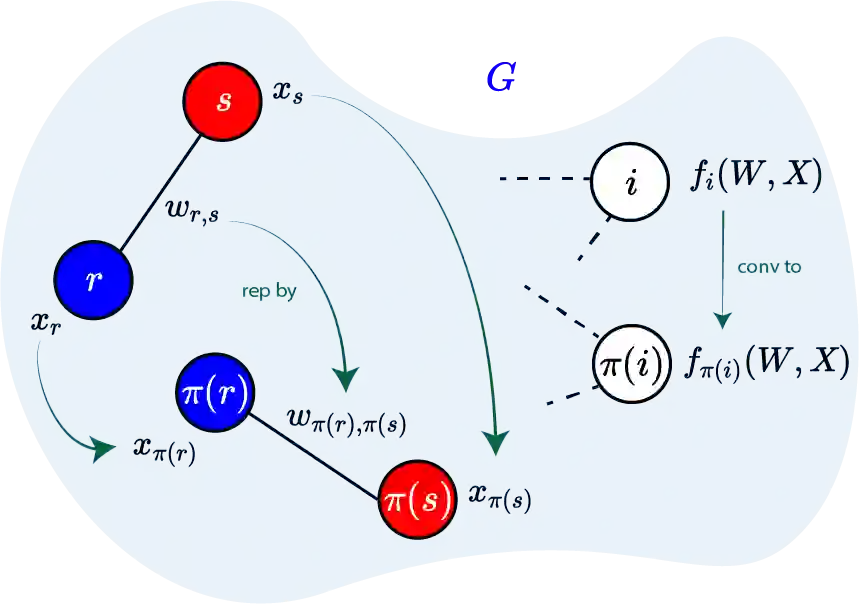
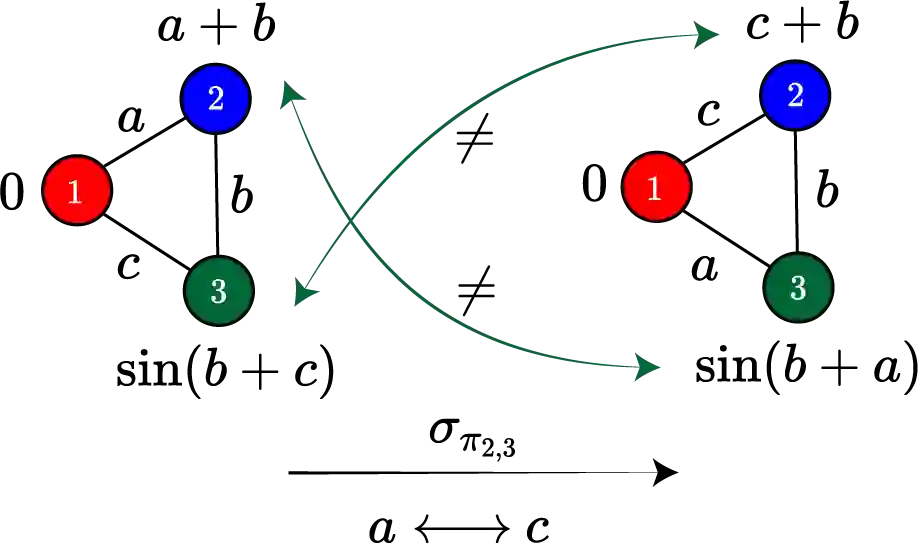
Given a graph function, defined on an arbitrary set of edge weights and node features, does there exist a Graph Neural Network (GNN) whose output is identical to the graph function? In this paper, we fully answer this question and characterize the class of graph problems that can be represented by GNNs. We identify an algebraic condition, in terms of the permutation of edge weights and node features, which proves to be necessary and sufficient for a graph problem to lie within the reach of GNNs. Moreover, we show that this condition can be efficiently verified by checking quadratically many constraints. Note that our refined characterization on the expressive power of GNNs are orthogonal to those theoretical results showing equivalence between GNNs and Weisfeiler-Lehman graph isomorphism heuristic. For instance, our characterization implies that many natural graph problems, such as min-cut value, max-flow value, and max-clique size, can be represented by a GNN. In contrast, and rather surprisingly, there exist very simple graphs for which no GNN can correctly find the length of the shortest paths between all nodes. Note that finding shortest paths is one of the most classical problems in Dynamic Programming (DP). Thus, the aforementioned negative example highlights the misalignment between DP and GNN, even though (conceptually) they follow very similar iterative procedures. Finally, we support our theoretical results by experimental simulations.