Gradient-Based Quantification of Epistemic Uncertainty for Deep Object Detectors

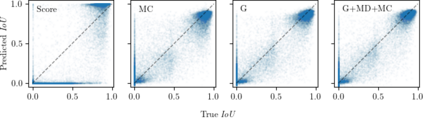
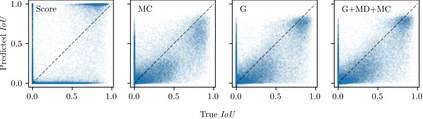
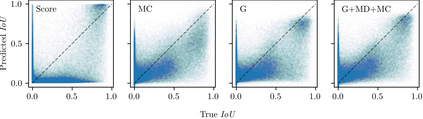
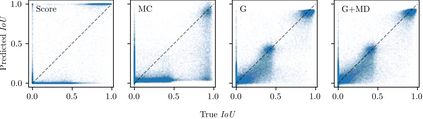
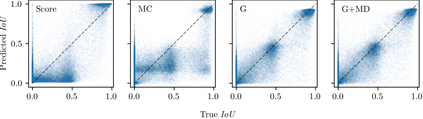
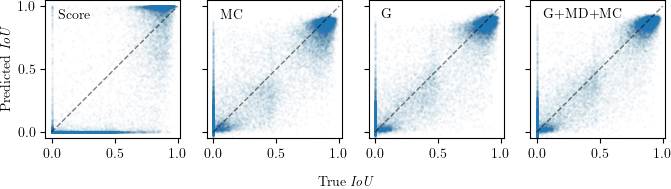
Reliable epistemic uncertainty estimation is an essential component for backend applications of deep object detectors in safety-critical environments. Modern network architectures tend to give poorly calibrated confidences with limited predictive power. Here, we introduce novel gradient-based uncertainty metrics and investigate them for different object detection architectures. Experiments on the MS COCO, PASCAL VOC and the KITTI dataset show significant improvements in true positive / false positive discrimination and prediction of intersection over union as compared to network confidence. We also find improvement over Monte-Carlo dropout uncertainty metrics and further significant boosts by aggregating different sources of uncertainty metrics.The resulting uncertainty models generate well-calibrated confidences in all instances. Furthermore, we implement our uncertainty quantification models into object detection pipelines as a means to discern true against false predictions, replacing the ordinary score-threshold-based decision rule. In our experiments, we achieve a significant boost in detection performance in terms of mean average precision. With respect to computational complexity, we find that computing gradient uncertainty metrics results in floating point operation counts similar to those of Monte-Carlo dropout.