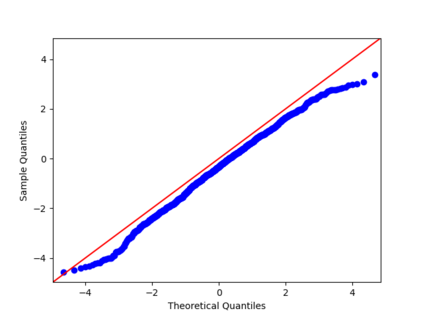
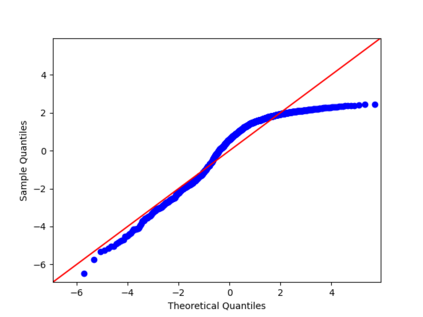
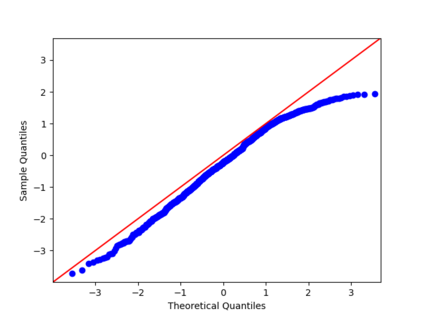
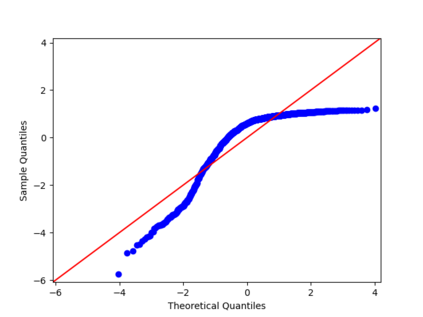
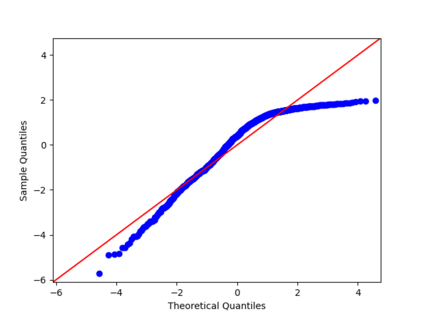
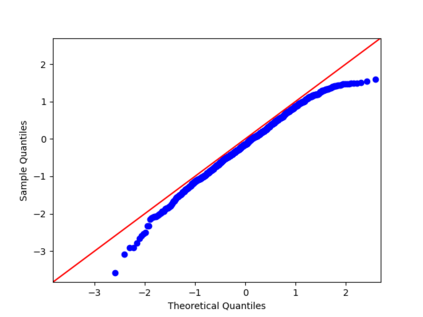
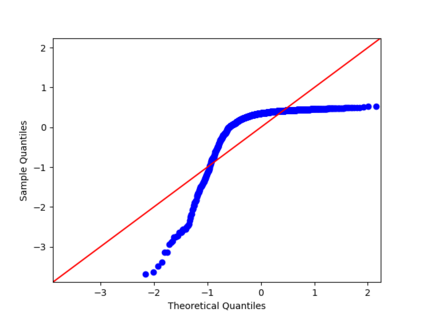
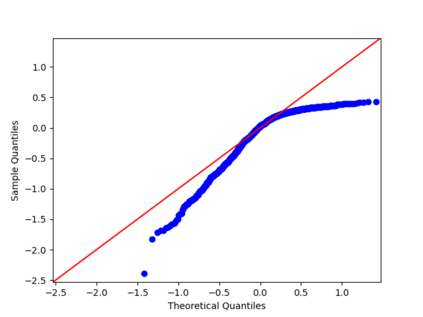
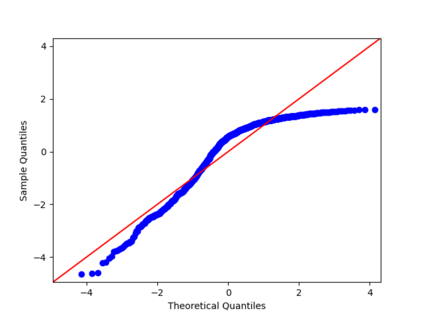
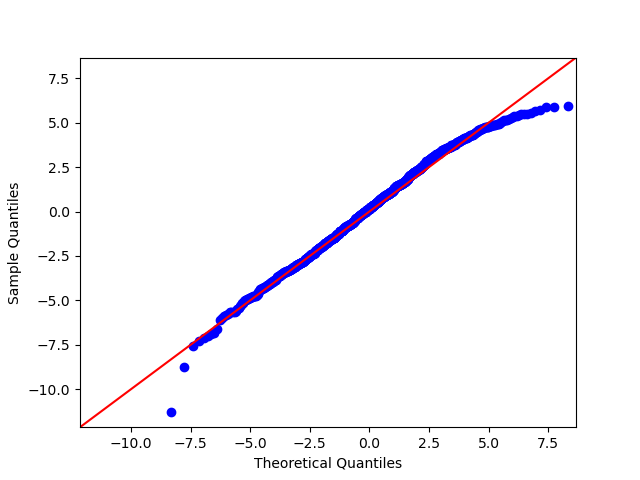
We propose a nonparametric estimator of the jump activity index $\beta$ of a pure-jump semimartingale $X$ driven by a $\beta$-stable process when the underlying observations are coming from a high-frequency setting at irregular times. The proposed estimator is based on an empirical characteristic function using rescaled increments of $X$, with a limit which depends in a complicated way on $\beta$ and the distribution of the sampling scheme. Utilising an asymptotic expansion we derive a consistent estimator for $\beta$ and prove an associated central limit theorem.
翻译:我们建议对跳跃活动指数的非参数估计值为$\beta$,这是由美元/beta$- sable过程驱动的纯跳跃半成形半成形美元X$的非参数估计值,如果基本观测来自非正常时间的高频环境,则该估计值基于经验特性函数,使用重估的X美元递增,其限度以美元/beta$和抽样计划的分布为复杂程度。我们利用非现成的扩展,得出一个一致的美元/beta$估计值,并证明一个相关的中心限值。