Symplectic Gaussian Process Dynamics

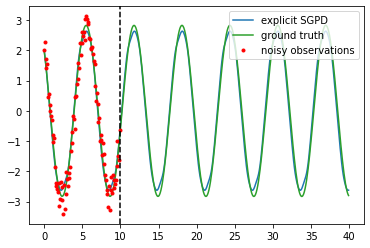
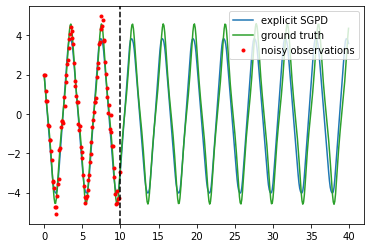
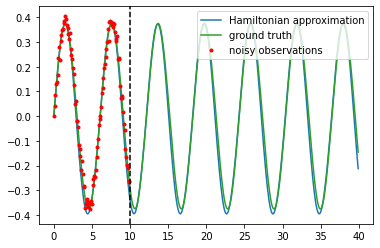
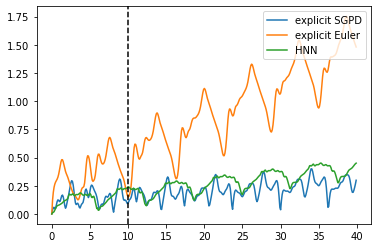
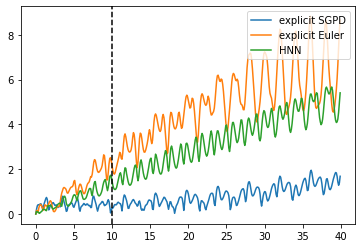
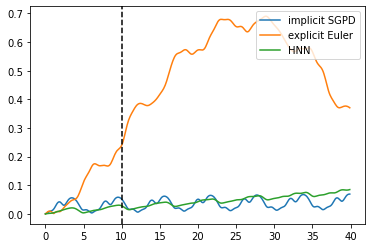
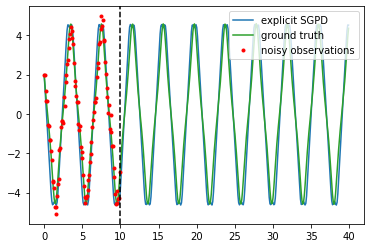
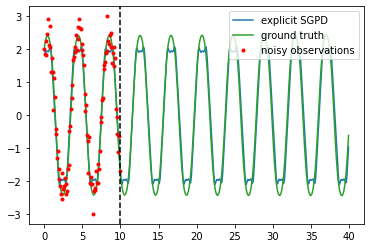
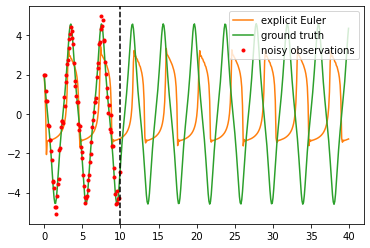
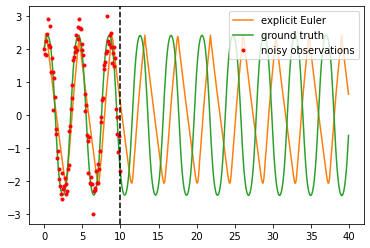
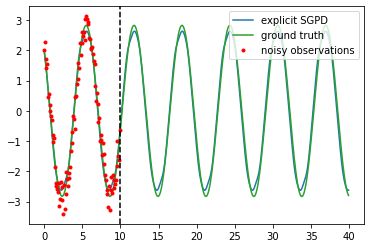
Dynamics model learning is challenging and at the same time an active field of research. Due to potential safety critical downstream applications, such as control tasks, there is a need for theoretical guarantees. While GPs induce rich theoretical guarantees as function approximators in space, they do not explicitly cope with the time aspect of dynamical systems. However, propagating system properties through time is exactly what classical numerical integrators were designed for. We introduce a recurrent sparse Gaussian process based variational inference scheme that is able to discretize the underlying system with any explicit or implicit single or multistep integrator, thus leveraging properties of numerical integrators. In particular we discuss Hamiltonian problems coupled with symplectic integrators producing volume preserving predictions.