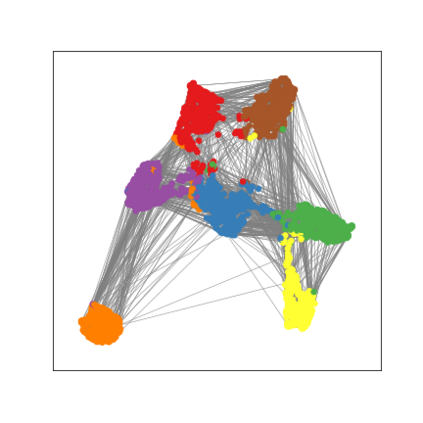
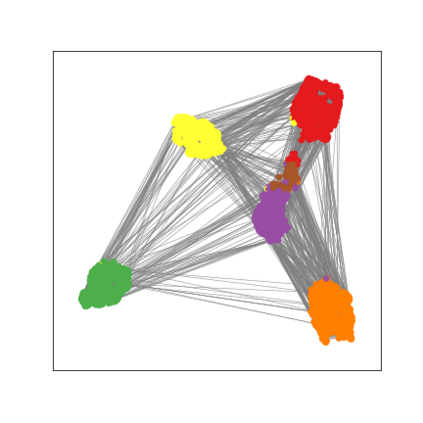
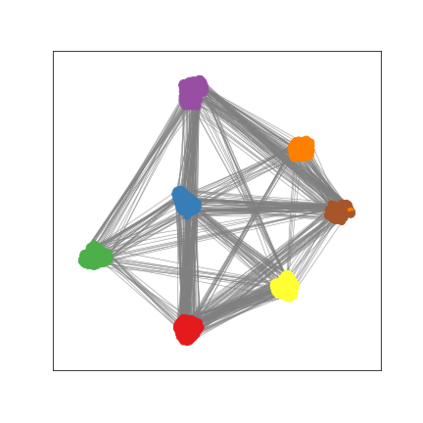
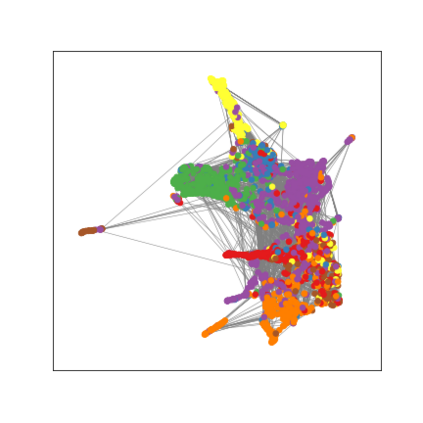
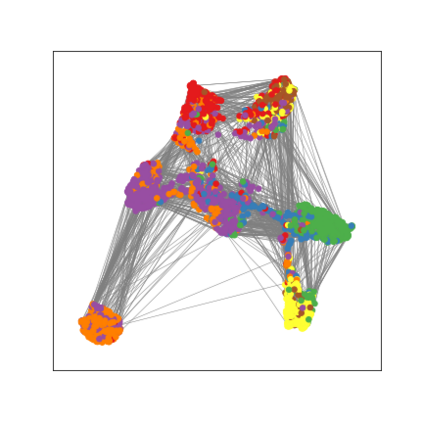
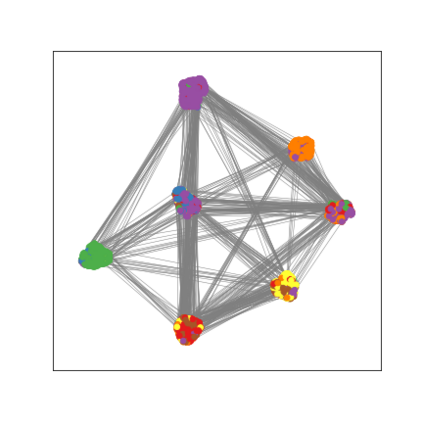
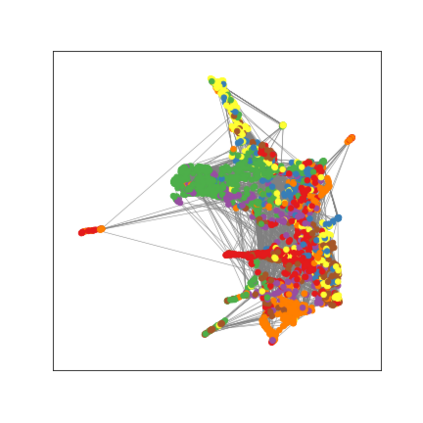
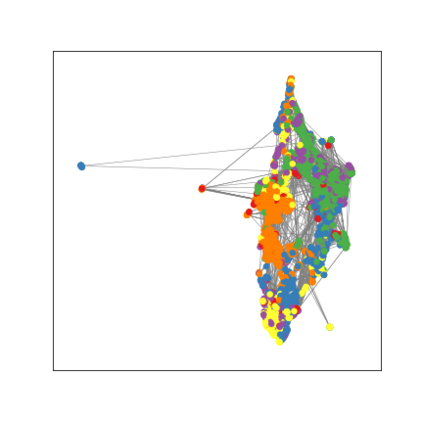
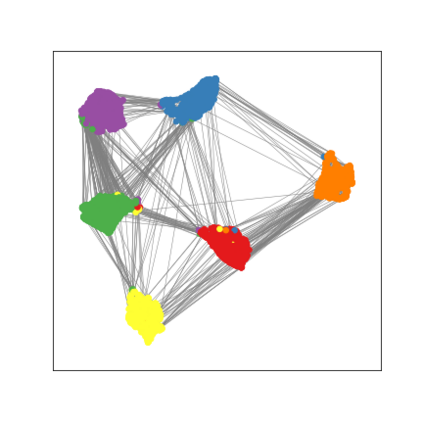
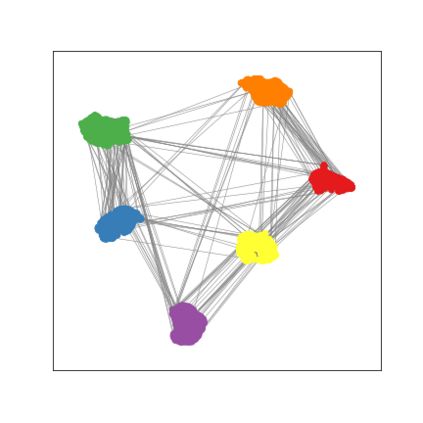
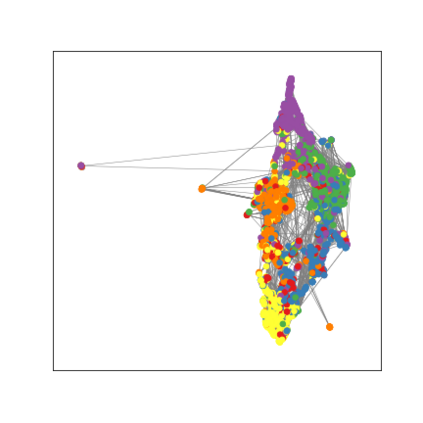
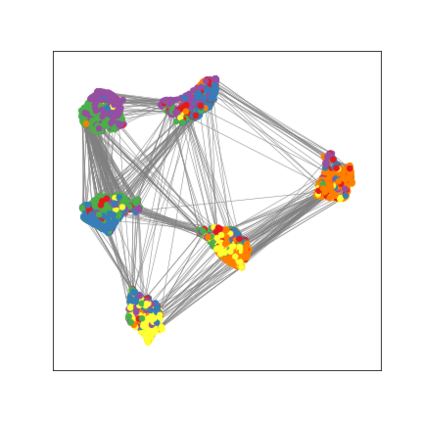
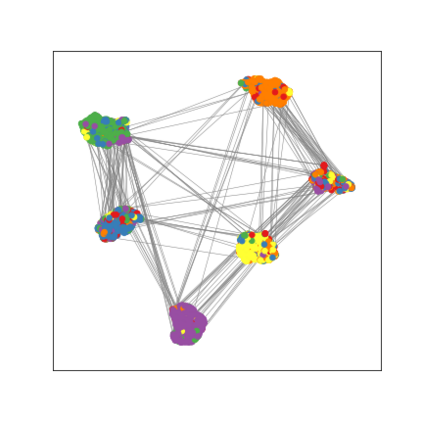
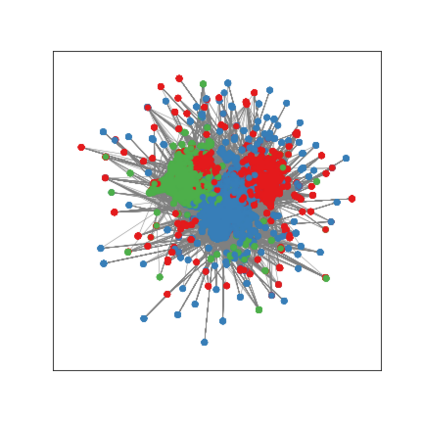
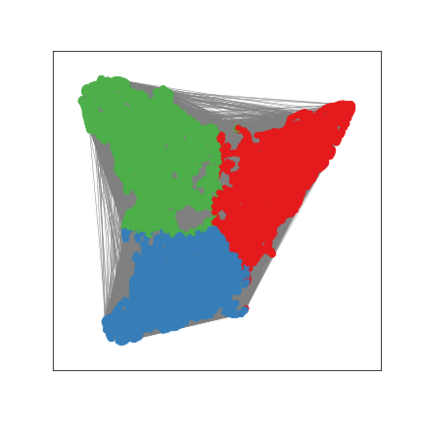
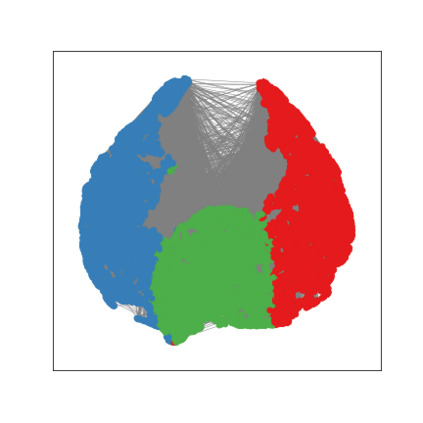
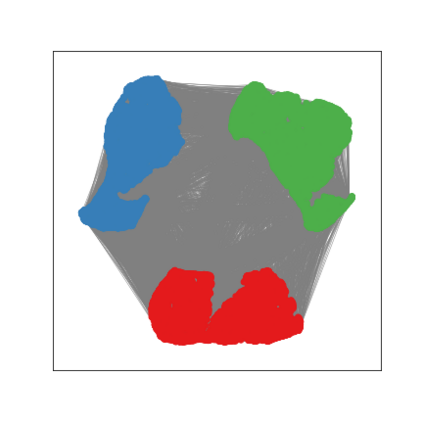
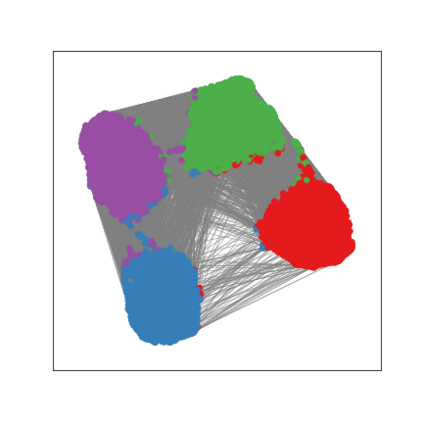
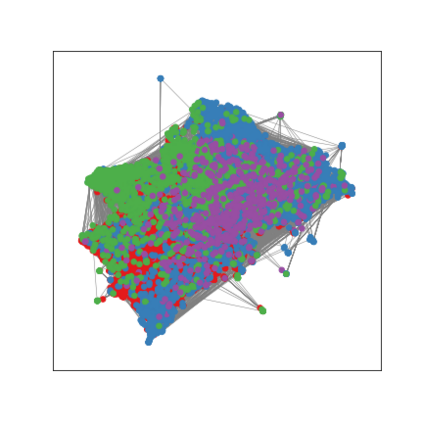
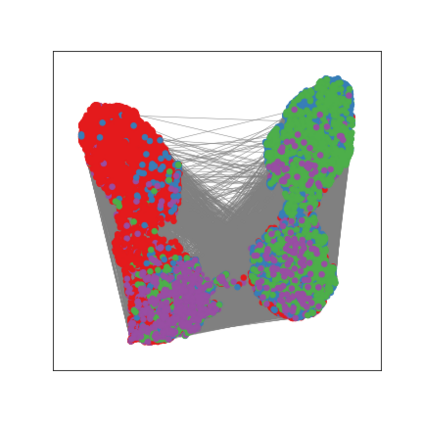
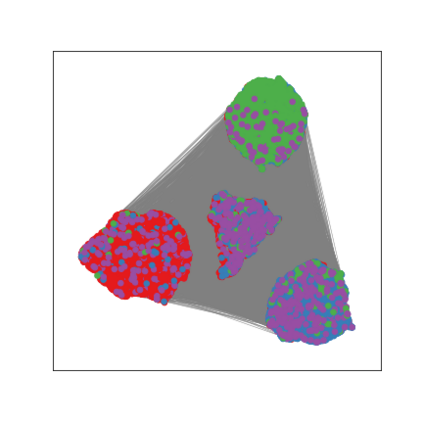
Graph Neural Networks (GNNs) are deep learning models designed to process attributed graphs. GNNs can compute cluster assignments accounting both for the vertex features and for the graph topology. Existing GNNs for clustering are trained by optimizing an unsupervised minimum cut objective, which is approximated by a Spectral Clustering (SC) relaxation. SC offers a closed-form solution that, however, is not particularly useful for a GNN trained with gradient descent. Additionally, the SC relaxation is loose and yields overly smooth cluster assignments, which do not separate well the samples. We propose a GNN model that optimizes a tighter relaxation of the minimum cut based on graph total variation (GTV). Our model has two core components: i) a message-passing layer that minimizes the $\ell_1$ distance in the features of adjacent vertices, which is key to achieving sharp cluster transitions; ii) a loss function that minimizes the GTV in the cluster assignments while ensuring balanced partitions. By optimizing the proposed loss, our model can be self-trained to perform clustering. In addition, our clustering procedure can be used to implement graph pooling in deep GNN architectures for graph classification. Experiments show that our model outperforms other GNN-based approaches for clustering and graph pooling.
翻译:神经网络(GNNs)是用于处理推算图的深层次学习模型。 GNNs可以计算用于顶端特征和图形表层的集群任务。 现有的用于分组的GNNs通过优化一个不受监督的最低切分目标来培训, 以光谱组合(SC) 松动为近处脊椎的距离为近处脊椎的最小截断目标为近处。 SC 提供了一个封闭式解决方案, 但对于受过梯度下降训练的GNN没有特别有用 。 此外, SC 放松松散, 产生过于平滑的集群任务, 并不将样本分开。 我们提议了一个基于图形总变异( GTV) 优化最小切分解的集群任务。 我们的GNNNS 模型有两个核心组成部分: i) 信息通路段, 将邻近脊椎的距离降到最低, $/ ell_ 1美元, 这是实现清晰的集群转换的关键; i) 损失功能, 最大限度地减少集群任务中的GTV, 同时确保平衡的分区分配。通过优化拟议的损失, 我们的模型可以自我训练来进行分组。 此外, 我们的模型的模型可以用来进行分组组合。 此外, 我们的GNNNNU的模型用于实施其他的G的G的模型的GGG的模型。