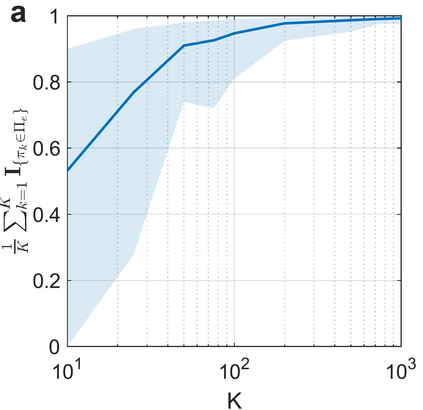
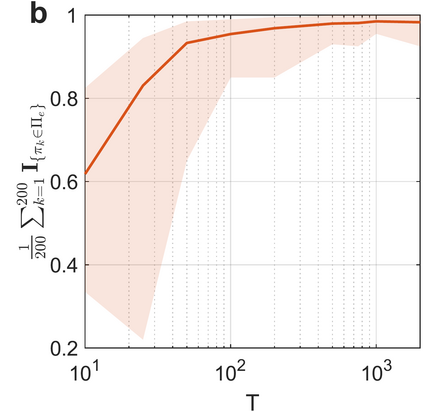
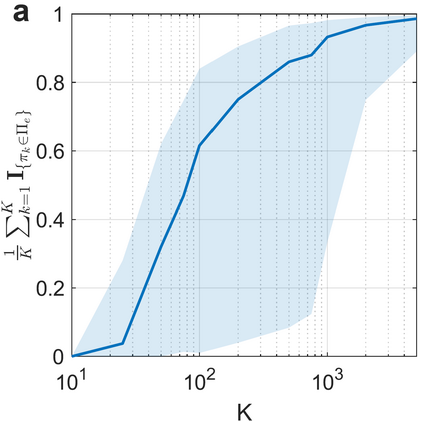
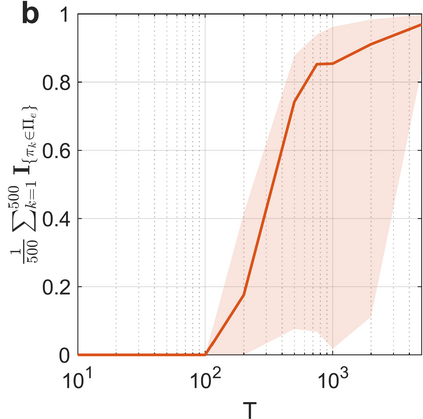
Learning in stochastic games is arguably the most standard and fundamental setting in multi-agent reinforcement learning (MARL). In this paper, we consider decentralized MARL in stochastic games in the non-asymptotic regime. In particular, we establish the finite-sample complexity of fully decentralized Q-learning algorithms in a significant class of general-sum stochastic games (SGs) - weakly acyclic SGs, which includes the common cooperative MARL setting with an identical reward to all agents (a Markov team problem) as a special case. We focus on the practical while challenging setting of fully decentralized MARL, where neither the rewards nor the actions of other agents can be observed by each agent. In fact, each agent is completely oblivious to the presence of other decision makers. Both the tabular and the linear function approximation cases have been considered. In the tabular setting, we analyze the sample complexity for the decentralized Q-learning algorithm to converge to a Markov perfect equilibrium (Nash equilibrium). With linear function approximation, the results are for convergence to a linear approximated equilibrium - a new notion of equilibrium that we propose - which describes that each agent's policy is a best reply (to other agents) within a linear space. Numerical experiments are also provided for both settings to demonstrate the results.
翻译:在多试剂强化学习(MARL)中,人们可以认为,在多试剂强化学习(MARL)中,学习运动可以说是最标准、最根本的环境。在本文中,我们考虑将MARL分散在非消毒制度中的随机游戏中。特别是,我们将完全分散的Q-学习算法在相当的普通和随机游戏(SGs)(SGs)中确定为有限的复杂性。在表格中,我们分析分散的Q-学习算法的样本复杂性,以便与所有试剂(Markov团队问题)的完全平衡(Nash均衡)相匹配。我们注重的是完全分散的MARL的实用而具有挑战性的设置,因为每个试剂都无法观察到完全分散的MARL的奖励或其他代理商的行为。事实上,每个代理商都完全忽略了其他决策者的存在。表式和线性函数近似案例都得到了考虑。在表格中,我们分析分散的Q-学习算法的样本复杂性,以便与Markov 完美平衡(Nash 平衡) 。线性函数近近似,结果是与线性平衡的趋同线性平衡――一种我们提出的平衡论中的一种新概念,它也是向其他代理商的一种对平衡的一种解释。