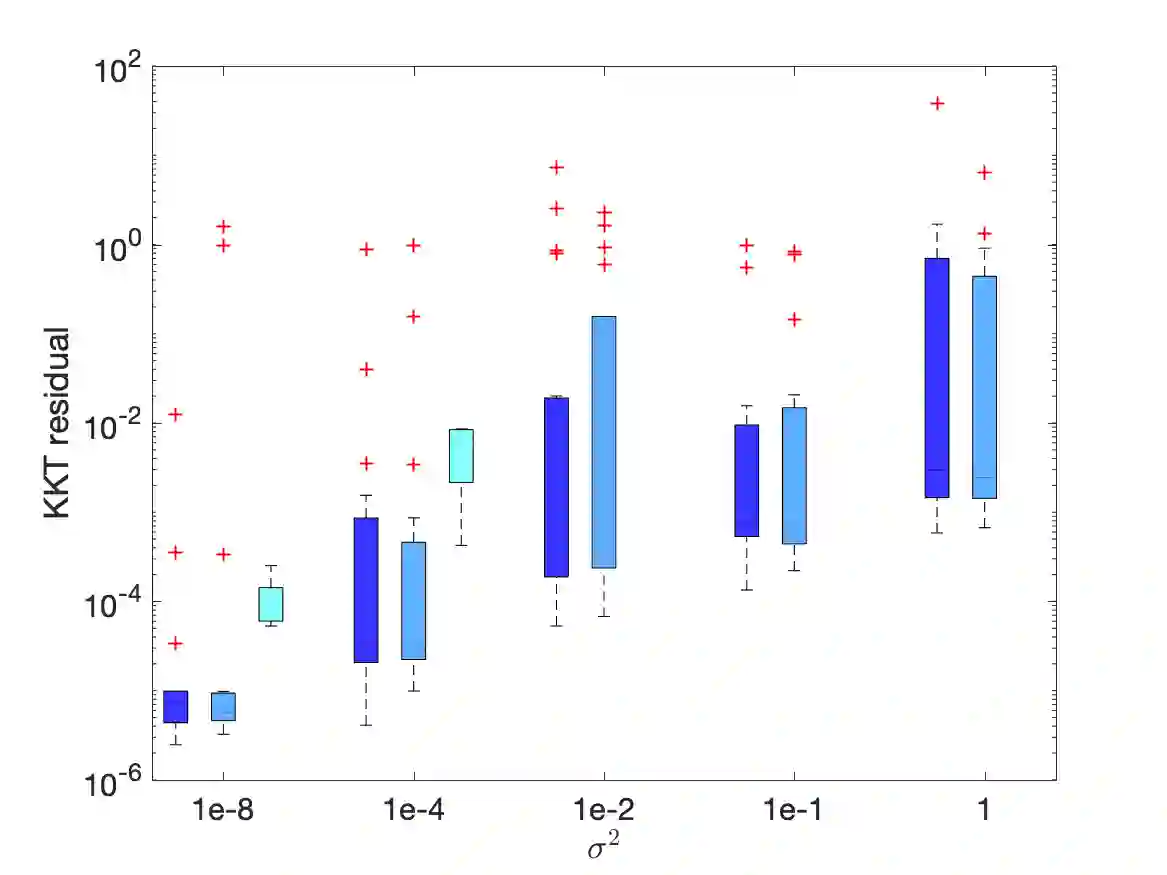
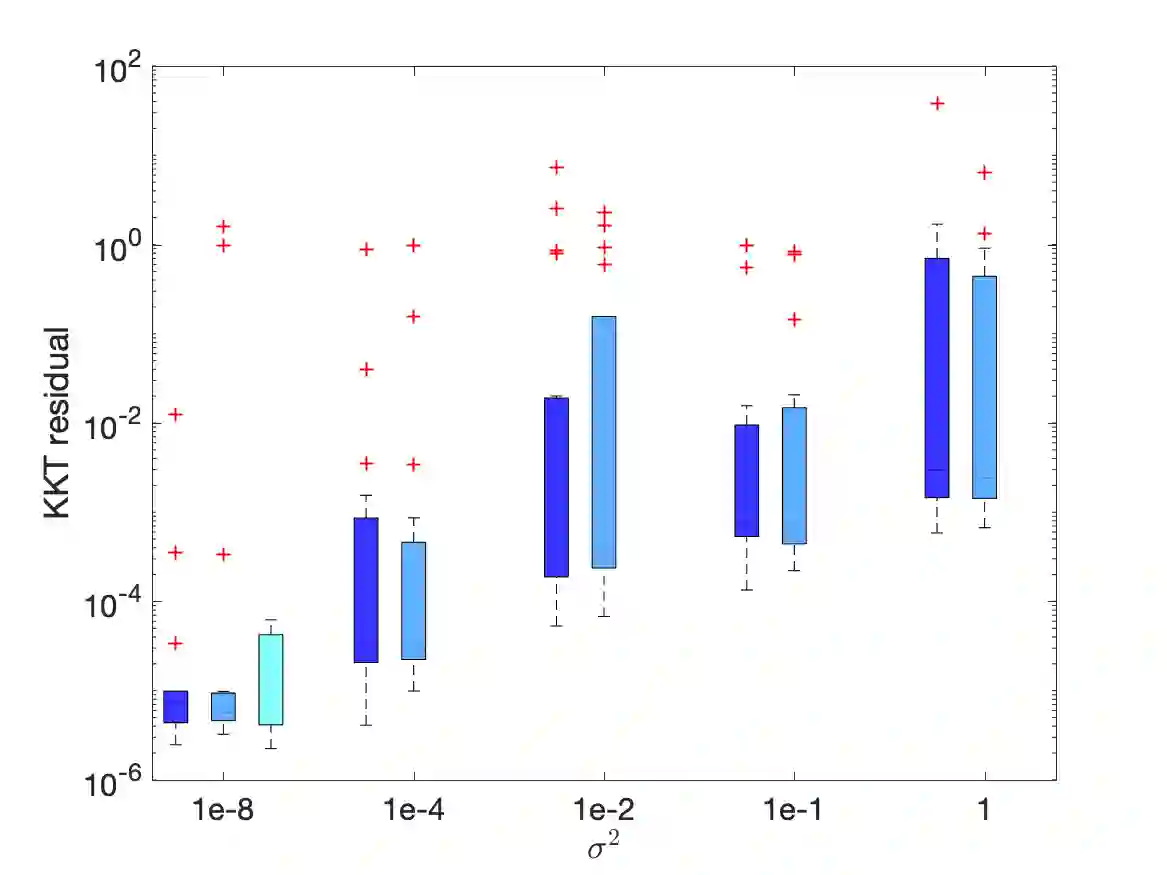
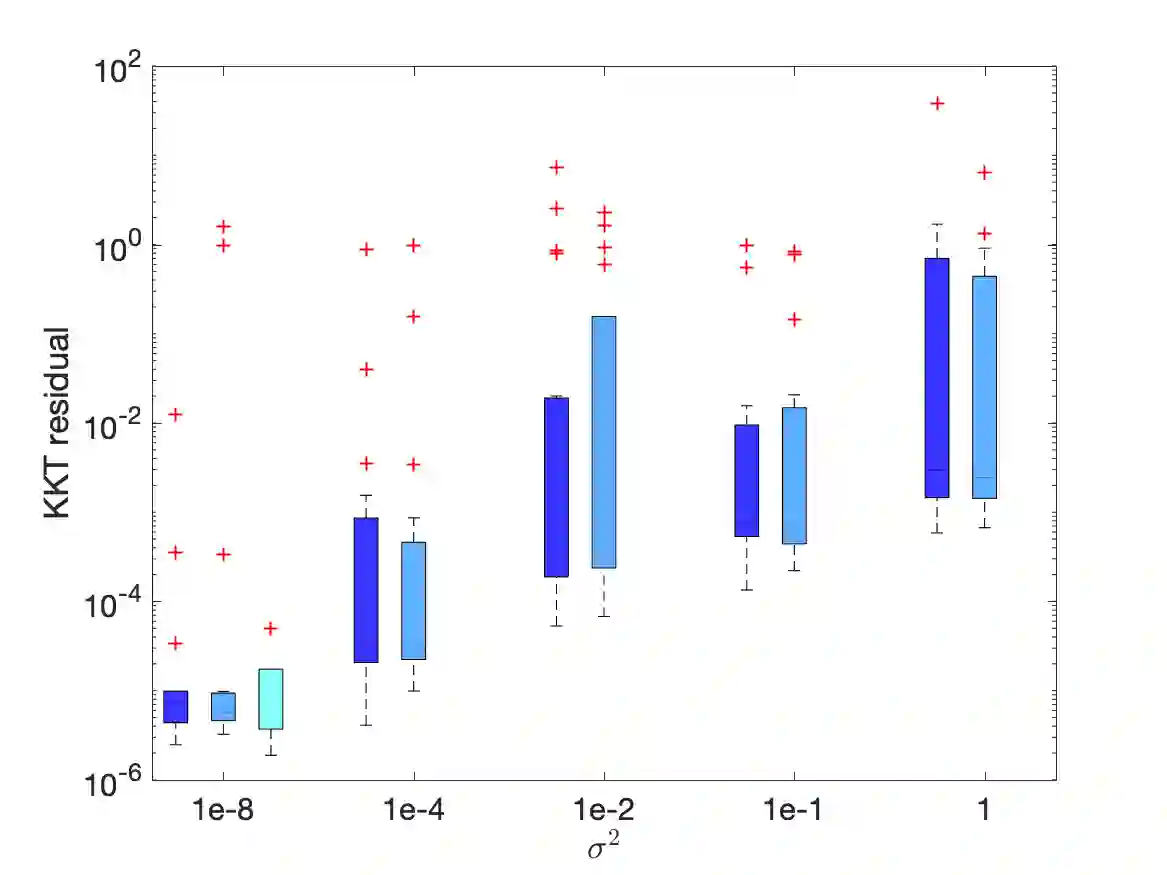
We study nonlinear optimization problems with stochastic objective and deterministic equality and inequality constraints, which emerge in numerous applications including finance, manufacturing, power systems and, recently, deep neural networks. We propose an active-set stochastic sequential quadratic programming algorithm, using a differentiable exact augmented Lagrangian as the merit function. The algorithm adaptively selects the penalty parameters of augmented Lagrangian and performs stochastic line search to decide the stepsize. The global convergence is established: for any initialization, the "liminf" of the KKT residuals converges to zero almost surely. Our algorithm and analysis further develop the prior work \cite{Na2021Adaptive} by allowing nonlinear inequality constraints. We demonstrate the performance of the algorithm on a subset of nonlinear problems collected in the CUTEst test set.
翻译:我们研究的是非线性优化问题,这些问题涉及随机客观和确定性平等以及不平等的限制,这些问题出现在金融、制造业、电力系统和最近的深神经网络等许多应用中。我们建议采用一种主动设置的随机连续二次二次二次编程算法,使用一种截然不同的精确增强的拉格朗江语作为功绩函数。算法通过适应性选择增强拉格朗江语的处罚参数,并进行随机搜索以决定步骤化。全球趋同已经确立:对于任何初始化,KKT残留物的“liminf”几乎可以肯定地归结为零。我们的算法和分析通过允许非线性不平等限制进一步开发了先前的工作 \ cite{Na2021Adaptition}。我们展示了CUTEst测试集收集的非线性问题组的算法的运作情况。