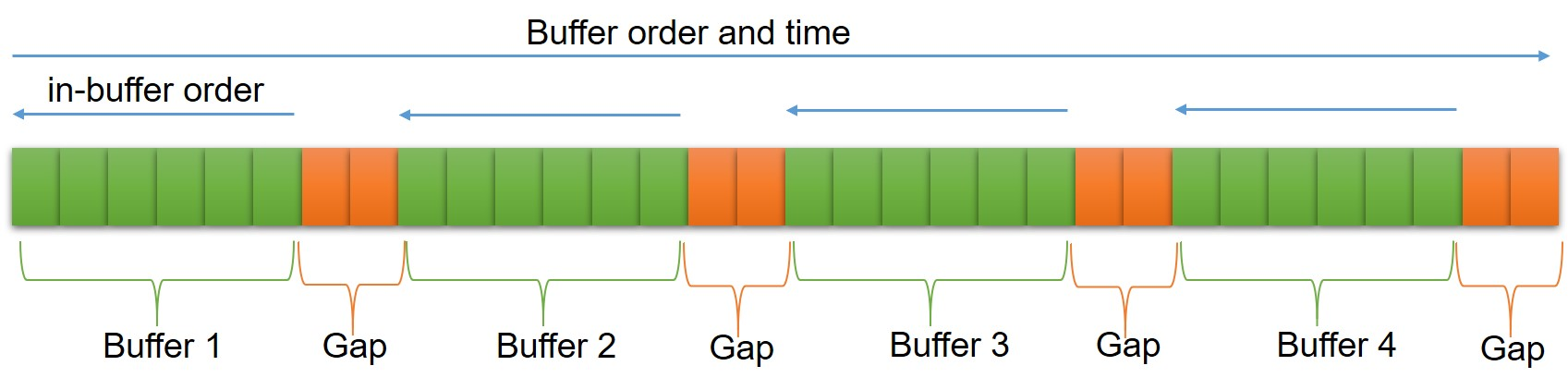
We consider the problem of estimating a linear time-invariant (LTI) dynamical system from a single trajectory via streaming algorithms, which is encountered in several applications including reinforcement learning (RL) and time-series analysis. While the LTI system estimation problem is well-studied in the {\em offline} setting, the practically important streaming/online setting has received little attention. Standard streaming methods like stochastic gradient descent (SGD) are unlikely to work since streaming points can be highly correlated. In this work, we propose a novel streaming algorithm, SGD with Reverse Experience Replay ($\mathsf{SGD}-\mathsf{RER}$), that is inspired by the experience replay (ER) technique popular in the RL literature. $\mathsf{SGD}-\mathsf{RER}$ divides data into small buffers and runs SGD backwards on the data stored in the individual buffers. We show that this algorithm exactly deconstructs the dependency structure and obtains information theoretically optimal guarantees for both parameter error and prediction error. Thus, we provide the first -- to the best of our knowledge -- optimal SGD-style algorithm for the classical problem of linear system identification with a first order oracle. Furthermore, $\mathsf{SGD}-\mathsf{RER}$ can be applied to more general settings like sparse LTI identification with known sparsity pattern, and non-linear dynamical systems. Our work demonstrates that the knowledge of data dependency structure can aid us in designing statistically and computationally efficient algorithms which can "decorrelate" streaming samples.
翻译:我们认为,通过流动算法从单一轨迹上估算线性时差(LTI)动态系统(LTI)的问题,这在几个应用程序中都遇到,包括强化学习(RL)和时间序列分析。虽然LTI系统估算问题在 {em 离线} 设置中得到了很好研究,但实际上重要的流流/线设置却很少受到注意。标准流方法,如Stochacific 梯度下行(SGD)不太可能发挥作用,因为流点可以是高度关联的。在这项工作中,我们提出一个新的流算法,SGD与逆向经验重放($\mathsf{SGD}-mathslevoral-lational-reslance Reviewority Reviews (Sgal-ral-ral-ral-ral-ral-ral-ral-ral-rent-ral-rent-ral-ral-lent-ral-rent-l-lent-ral-l-l-l-l-lent-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-l-