$H^1$-stability of an L2-type method on general nonuniform meshes for subdiffusion equation

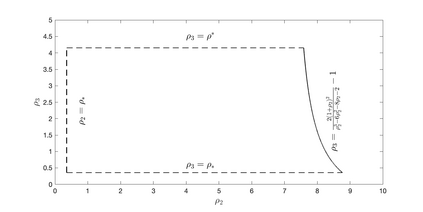
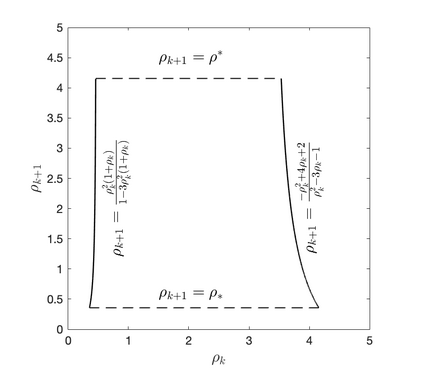
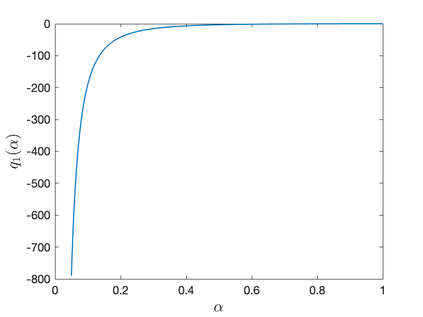
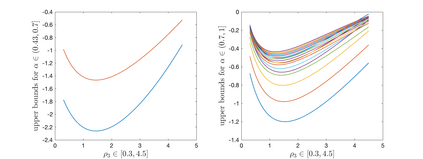
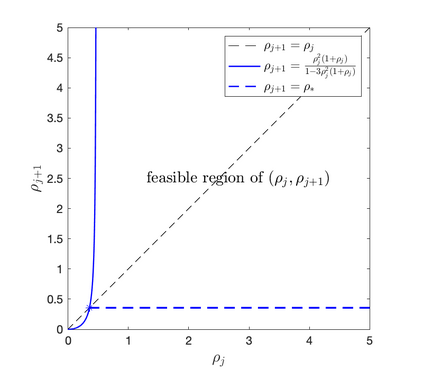
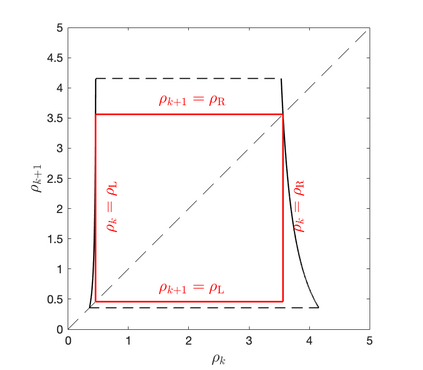
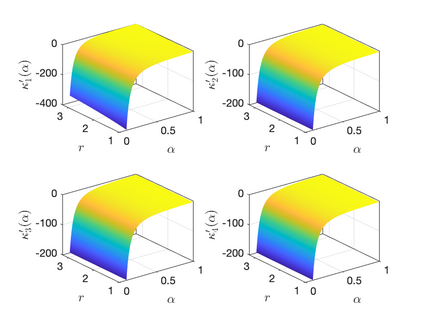
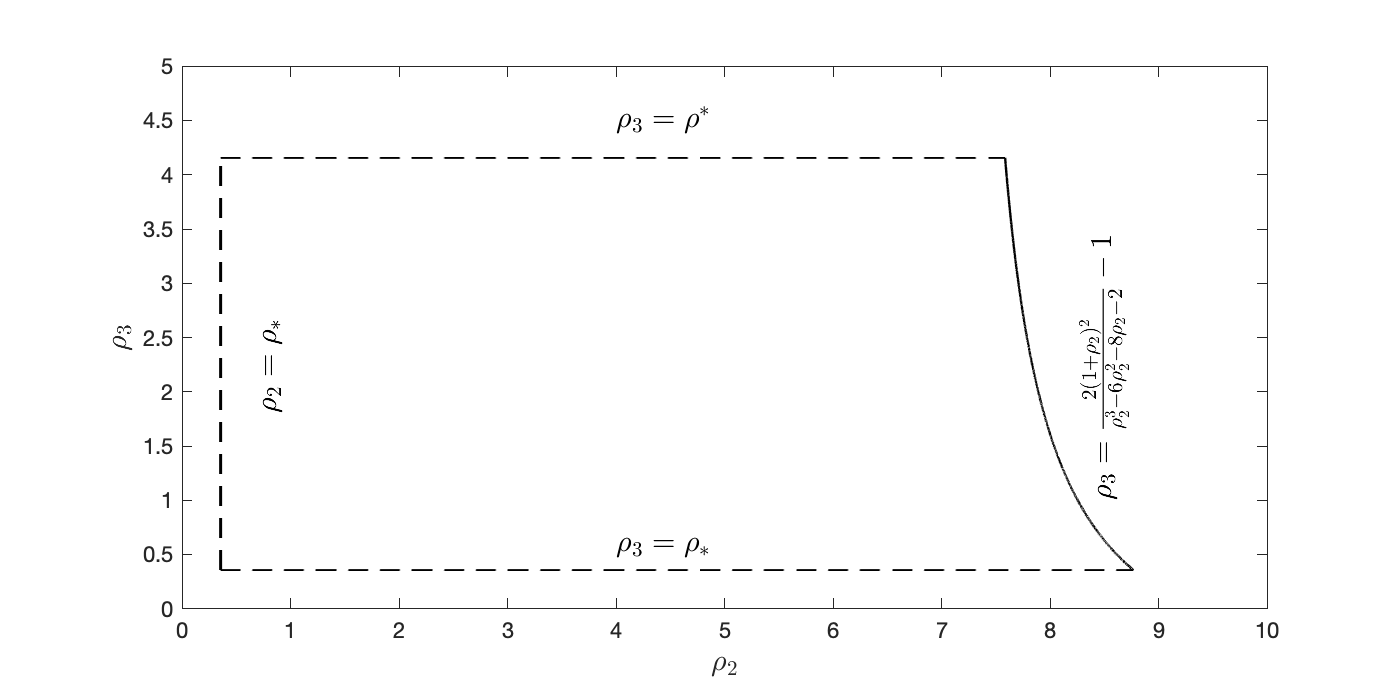
In this work the $H^1$-stability of an L2 method on general nonuniform meshes is established for the subdiffusion equation. Under some mild constraints on the time step ratio $\rho_k$, for example $0.4573328\leq \rho_k\leq 3.5615528$ for all $k\geq 2$, a crucial bilinear form associated with the L2 fractional-derivative operator is proved to be positive semidefinite. As a consequence, the $H^1$-stability of L2 schemes can be derived for the subdiffusion equation. In the special case of graded mesh, such positive semidefiniteness holds when the grading parameter $1<r\leq 3.2016538$ and therefore the $H^1$-stability of L2 schemes holds. To the best of our knowledge, this is the first work on the $H^1$-stability of L2 method on general nonuniform meshes for subdiffusion equation.