Bayesian clustering using random effects models and predictive projections

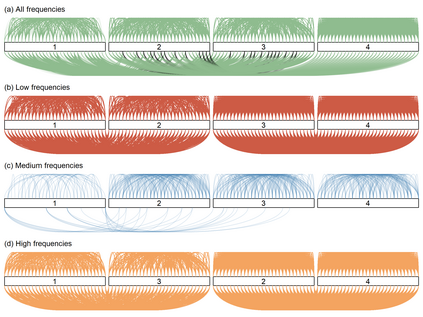
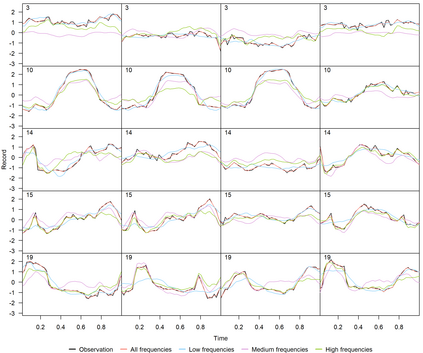
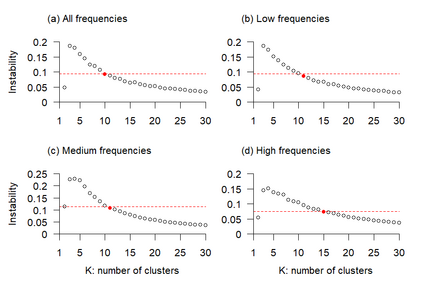
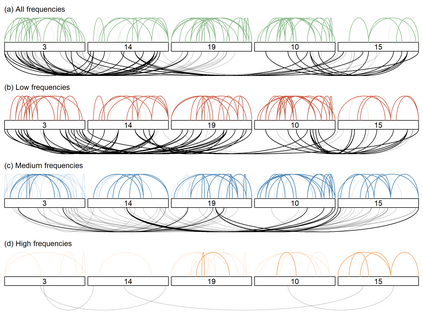
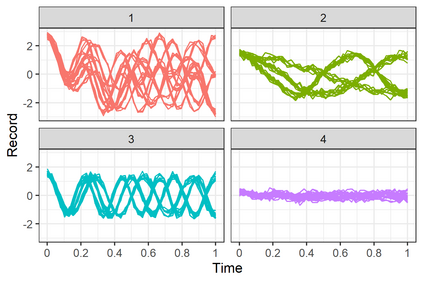
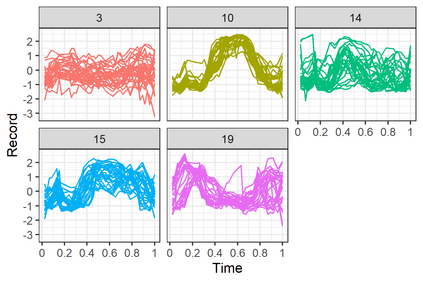
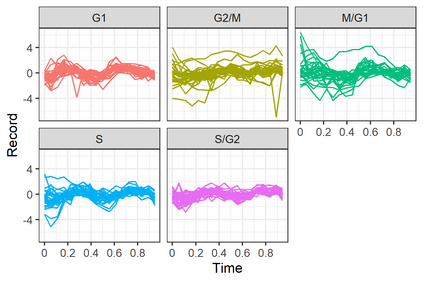
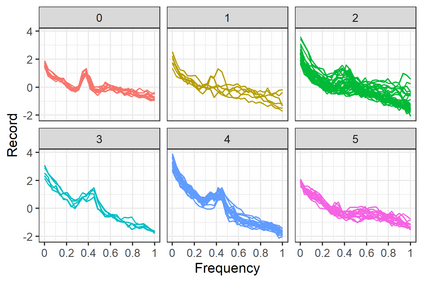
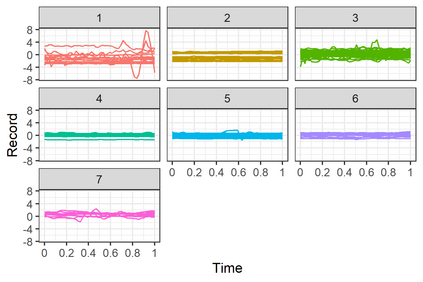
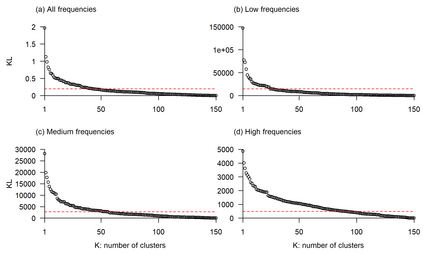
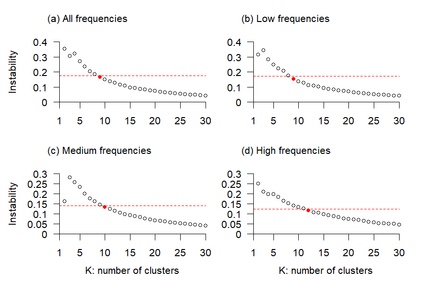
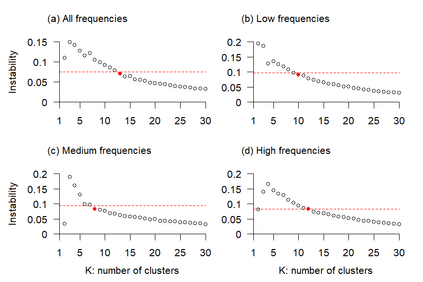
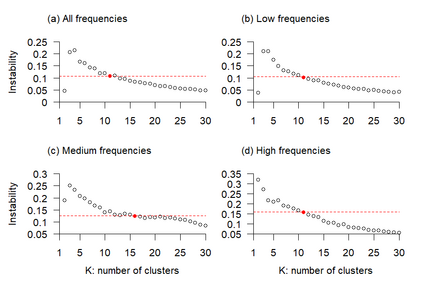
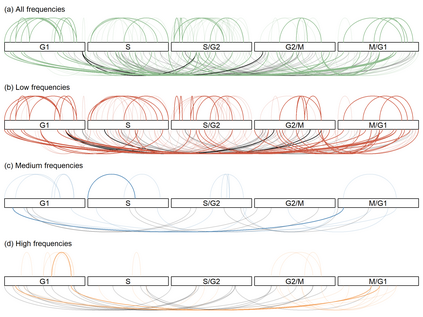
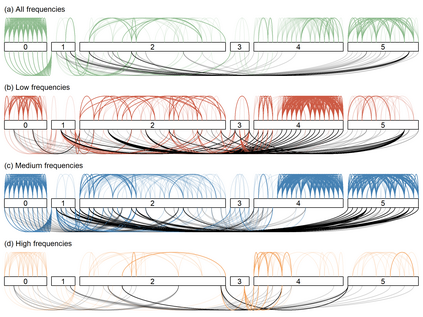
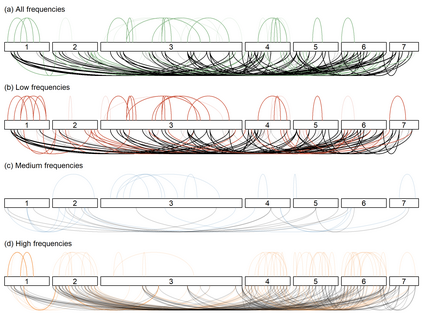
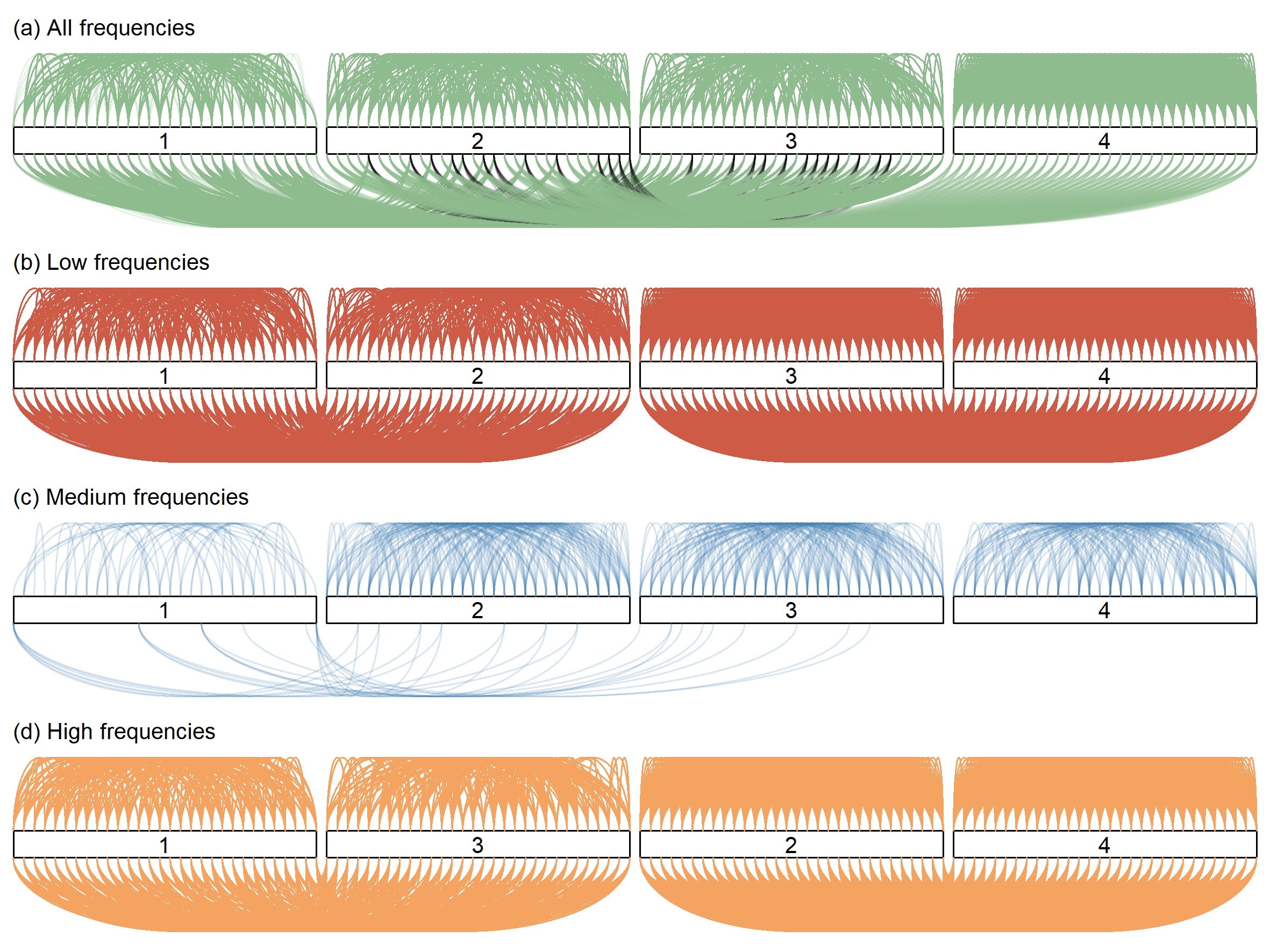
Linear mixed models are widely used for analyzing hierarchically structured data involving missingness and unbalanced study designs. We consider a Bayesian clustering method that combines linear mixed models and predictive projections. For each observation, we consider a predictive replicate in which only a subset of the random effects is shared between the observation and its replicate, with the remainder being integrated out using the conditional prior. Predictive projections are then defined in which the number of distinct values taken by the shared random effects is finite, in order to obtain different clusters. Integrating out some of the random effects acts as a noise filter, allowing the clustering to be focused on only certain chosen features of the data. The method is inspired by methods for Bayesian model checking, in which simulated data replicates from a fitted model are used for model criticism by examining their similarity to the observed data in relevant ways. Here the predictive replicates are used to define similarity between observations in relevant ways for clustering. To illustrate the way our method reveals aspects of the data at different scales, we consider fitting temporal trends in longitudinal data using Fourier cosine bases with a random effect for each basis function, and different clusterings defined by shared random effects for replicates of low or high frequency terms. The method is demonstrated in a series of real examples.