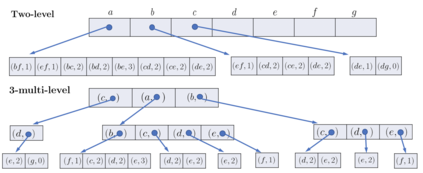
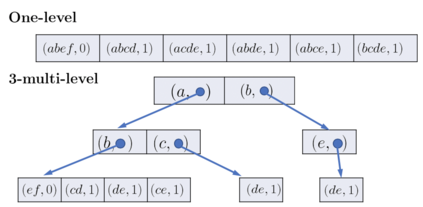
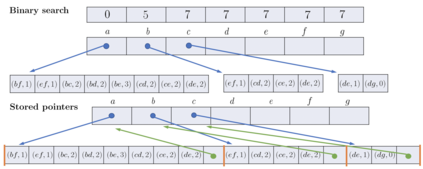
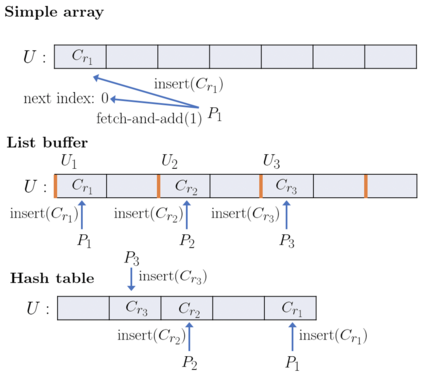
This paper studies the nucleus decomposition problem, which has been shown to be useful in finding dense substructures in graphs. We present a novel parallel algorithm that is efficient both in theory and in practice. Our algorithm achieves a work complexity matching the best sequential algorithm while also having low depth (parallel running time), which significantly improves upon the only existing parallel nucleus decomposition algorithm (Sariyuce et al., PVLDB 2018). The key to the theoretical efficiency of our algorithm is the use of a theoretically-efficient parallel algorithms for clique listing and bucketing. We introduce several new practical optimizations, including a new multi-level hash table structure to store information on cliques space-efficiently and a technique for traversing this structure cache-efficiently. On a 30-core machine with two-way hyper-threading on real-world graphs, we achieve up to a 55x speedup over the state-of-the-art parallel nucleus decomposition algorithm by Sariyuce et al., and up to a 40x self-relative parallel speedup. We are able to efficiently compute larger nucleus decompositions than prior work on several million-scale graphs for the first time.
翻译:本文研究核心分解问题, 事实证明, 核心分解问题对于在图表中找到密集的子结构是有用的。 我们展示了一种新的平行算法, 在理论和实践上都是高效的。 我们的算法实现了与最佳顺序算法相匹配的工作复杂性, 同时也具有低深度( 平行运行时间), 这极大地改善了唯一存在的平行核心分解算法( Sariyuce 等人, PVLDB 2018) 。 我们算法的理论效率的关键是使用一种理论上有效的平行相平行算法来进行分解和打桶。 我们引入了几种新的实用优化, 包括一个新的多级散货表结构, 以存储关于cliques的空间高效信息, 以及一种在结构缓存中穿行的技术。 在一台30个核心机器上, 双向超高读真实世界图形, 我们实现了55x速度的快速增长。 由Sariyuce 等人 等人( 等人) 和 向40x 自动平行的平行分解算法, 以及40x 平行的同步加速速度。 我们能够有效地进行前几百万次的分解的图像。