Rethinking the Funding Line at the Swiss National Science Foundation: Bayesian Ranking and Lottery

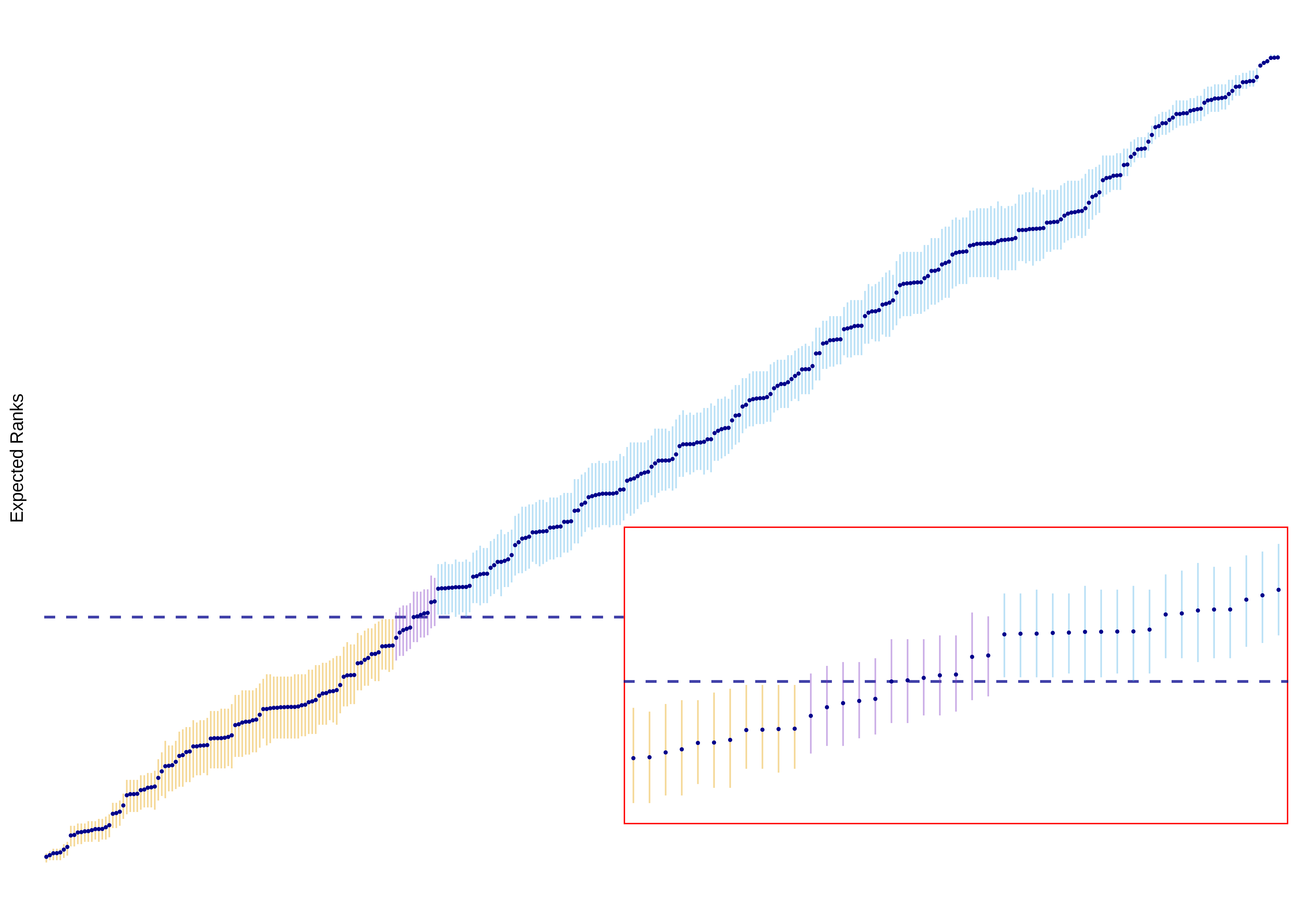
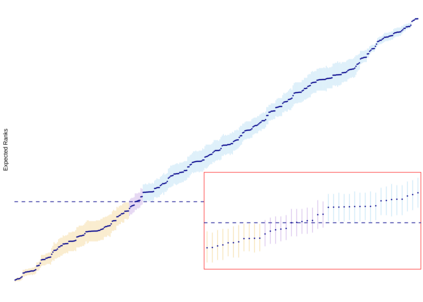
Funding agencies rely on peer review and expert panels to select the research deserving funding. Peer review has limitations, including bias against risky proposals or interdisciplinary research. The inter-rater reliability between reviewers and panels is low, particularly for proposals near the funding line. Funding agencies are also increasingly acknowledging the role of chance. The Swiss National Science Foundation (SNSF) introduced a lottery for proposals in the middle group of good but not excellent proposals. In this article, we introduce a Bayesian hierarchical model for the evaluation process. To rank the proposals, we estimate their expected ranks (ER), which incorporates both the magnitude and uncertainty of the estimated differences between proposals. A provisional funding line is defined based on ER and budget. The ER and its credible interval are used to identify proposals with similar quality and credible intervals that overlap with the funding line. These proposals are entered into a lottery. We illustrate the approach for two SNSF grant schemes in career and project funding. We argue that the method could reduce bias in the evaluation process. R code, data and other materials for this article are available online.