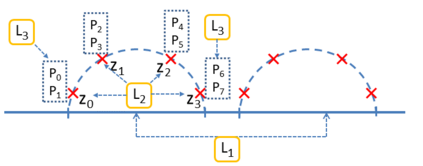
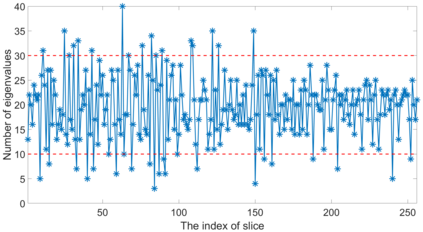
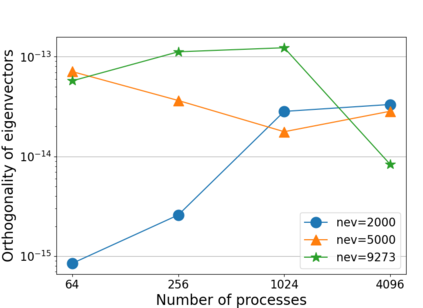
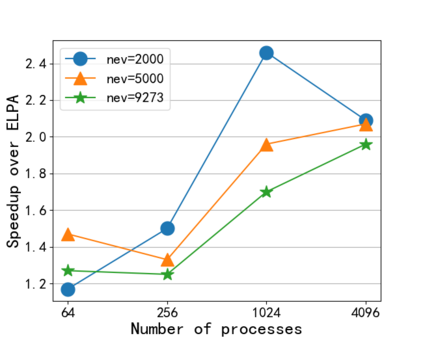
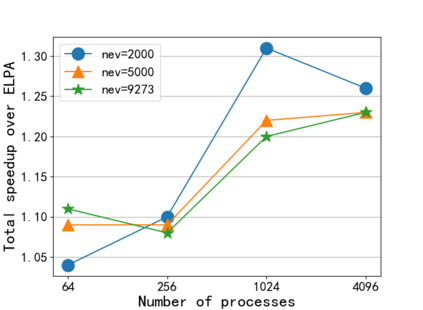
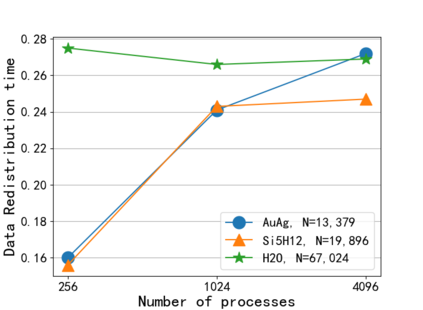
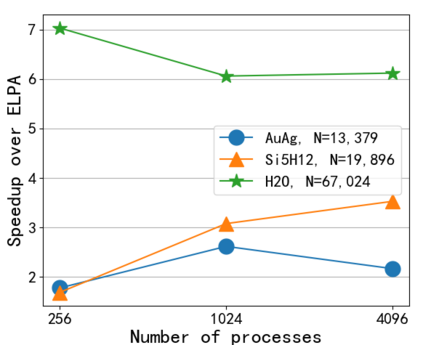
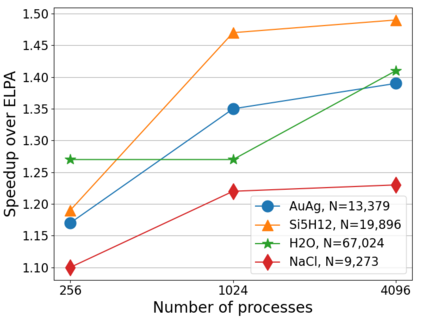
In this paper, a Parallel Direct Eigensolver for Sequences of Hermitian Eigenvalue Problems with no tridiagonalization is proposed, denoted by \texttt{PDESHEP}, and it combines direct methods with iterative methods. \texttt{PDESHEP} first reduces a Hermitian matrix to its banded form, then applies a spectrum slicing algorithm to the banded matrix, and finally computes the eigenvectors of the original matrix via backtransform. Therefore, compared with conventional direct eigensolvers, \texttt{PDESHEP} avoids tridiagonalization, which consists of many memory-bounded operations. In this work, the iterative method in \texttt{PDESHEP} is based on the contour integral method implemented in FEAST. The combination of direct methods with iterative methods for banded matrices requires some efficient data redistribution algorithms both from 2D to 1D and from 1D to 2D data structures. Hence, some two-step data redistribution algorithms are proposed, which can be $10\times$ faster than ScaLAPACK routine \texttt{PXGEMR2D}. For the symmetric self-consistent field (SCF) eigenvalue problems, \texttt{PDESHEP} can be on average $1.25\times$ faster than the state-of-the-art direct solver in ELPA when using $4096$ processes. Numerical results are obtained for dense Hermitian matrices from real applications and large real sparse matrices from the SuiteSparse collection.
翻译:在本文中, 推荐了 Exmitian Eigenval 问题序列的平行直导 EigenalSolver, 没有三维方位化, 由\ textt{PDESHEP} 表示, 并将直接方法与迭代方法相结合。\ textt{PDESHEP} 首先将 Hermitian 矩阵缩放为带状形式, 然后将频谱剪切算法应用到带宽矩阵中, 最后通过后变法对原始矩阵的序列序列进行解析。 因此, 与常规直接的egensoltvers 相比,\ textt{PDESHEP} 避免了由许多内存限制操作组成的三维方位化。 在这项工作中,\ textt{PDEHEDE} 的迭接合方法与带宽度矩阵的迭代方法相结合, 需要从 2D 到 1D 和 2D 数据结构中一些高效的数据再分配算法。 因此, 双级数据再配置数据流的 RDRDRDRD 算算算算法, 用于 $rental- scial- realdrevaldrevental kalalalalalx 。