Comparison of Azzalini and Geometric Skew Normal Distributions Under Bayesian Paradigm

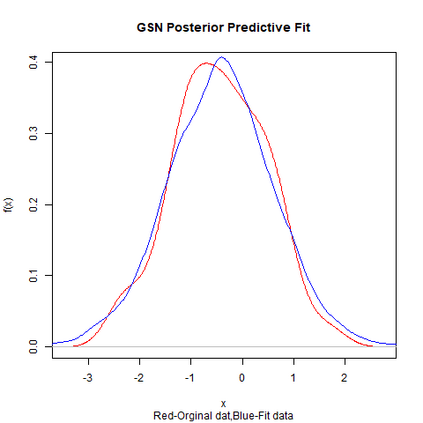
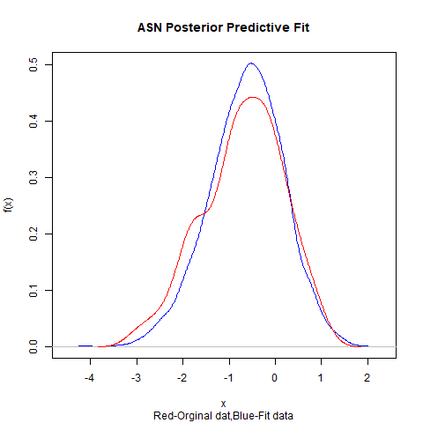
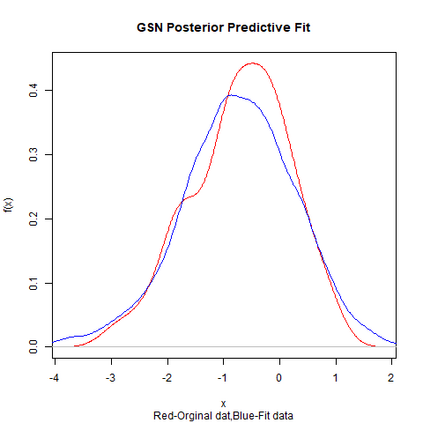
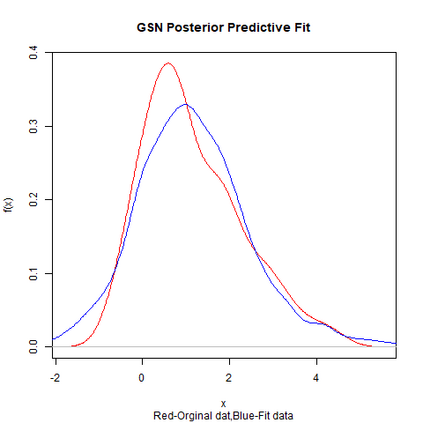
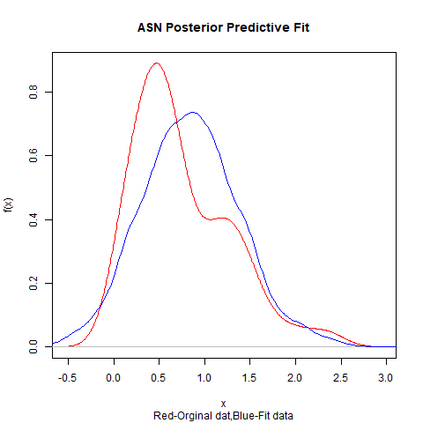
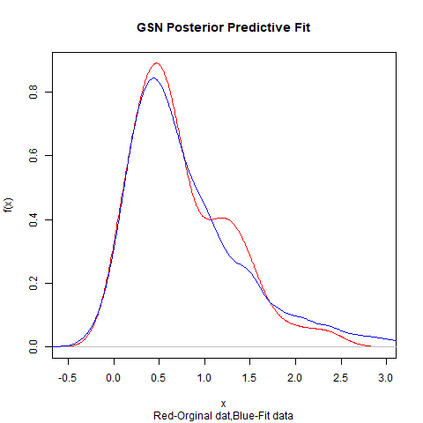
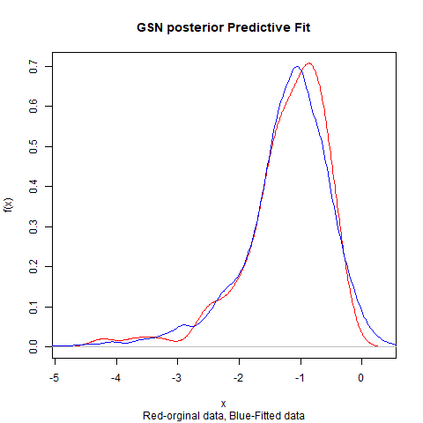
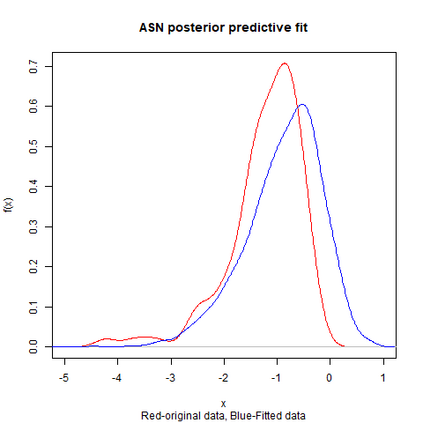
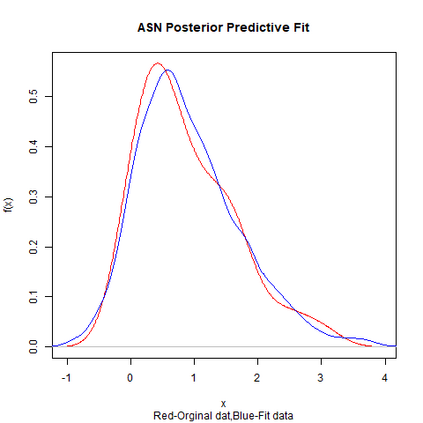
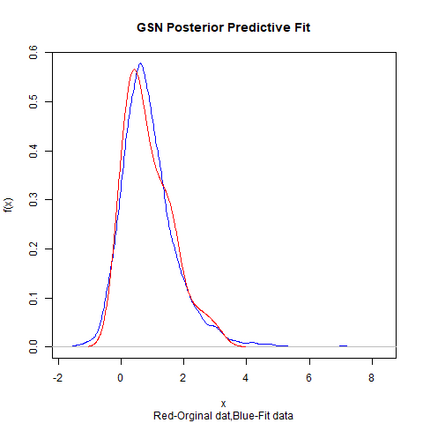
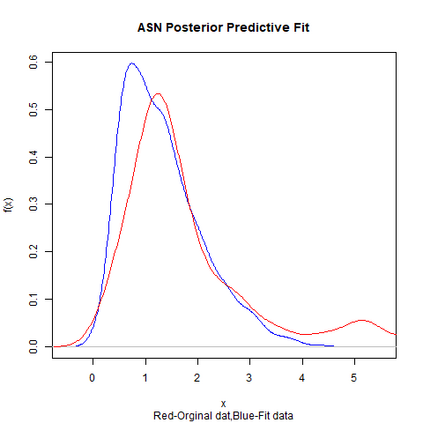
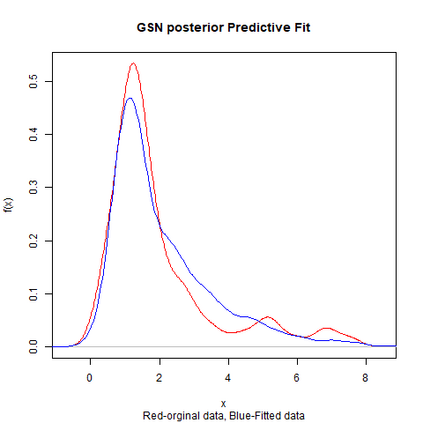
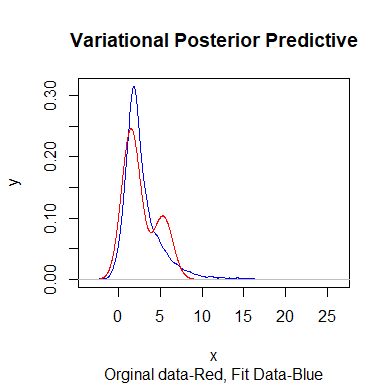
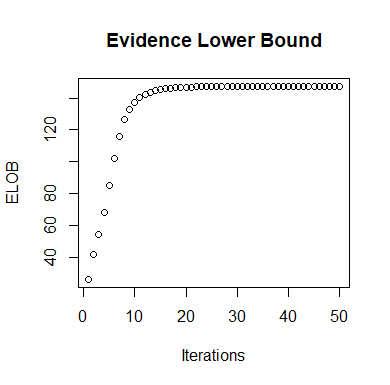
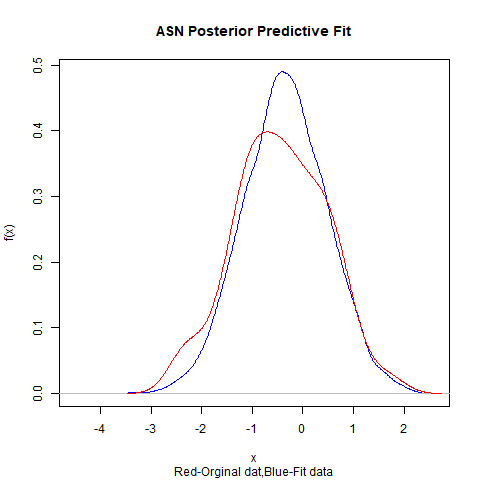
Skewed generalizations of the normal distribution have been a topic of great interest in the statistics community due to their diverse applications across several domains. One of the most popular skew normal distributions, due to its intuitive appeal, is the Azzalini's skew normal distribution. However, due to the nature of the distribution it suffers from serious inferential problems. Interestingly, the Bayesian approach has been shown to mitigate these issues. Recently, another skew normal distribution, the Geometric skew normal distribution, which is structurally different from Azzalini's skew normal distribution, has been proposed as an alternative for modelling skewed data. Despite the interest in skew normal distributions, a limited number of articles deal with comparing the performance of different skew distributions, especially in the Bayesian context. To address this gap, the article attempts to compare these two skew normal distributions in the Bayesian paradigm for modelling data with varied skewness. The posterior estimates of the parameters of the geometric skew normal distribution are obtained using a hybrid Gibbs-Metropolis algorithm and the posterior predictive fit to the data is also obtained. Similarly, for the Azzalini's skew normal distribution, the posterior predictive fit are derived using a Gibbs sampling algorithm. To compare the performance, Kolmogorov-Smirnov distance between the posterior predictive distribution and original data is utilised to measure the goodness of fit for both the models. An assortment of real and simulated data sets, with a wide range of skewness, are analyzed using both the models and the advantages as well as disadvantages of the two models are also discussed. Finally, a much faster Variational Bayes method for approximating the posterior distribution of the geometric skew normal model is proposed and its performance is discussed.