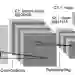
Full-physics cosmological simulations are powerful tools for studying the formation and evolution of structure in the universe but require extreme computational resources. Here, we train a convolutional neural network to use a cheaper N-body-only simulation to reconstruct the baryon hydrodynamic variables (density, temperature, and velocity) on scales relevant to the Lyman-$\alpha$ (Ly$\alpha$) forest, using data from Nyx simulations. We show that our method enables rapid estimation of these fields at a resolution of $\sim$20kpc, and captures the statistics of the Ly$\alpha$ forest with much greater accuracy than existing approximations. Because our model is fully-convolutional, we can train on smaller simulation boxes and deploy on much larger ones, enabling substantial computational savings. Furthermore, as our method produces an approximation for the hydrodynamic fields instead of Ly$\alpha$ flux directly, it is not limited to a particular choice of ionizing background or mean transmitted flux.
翻译:全物理宇宙模拟是研究宇宙结构形成和演变的有力工具,但需要极端的计算资源。在这里,我们训练一个革命性神经网络,使用更便宜的N-体模拟,以重建与莱曼-$(利元/阿尔法元)森林有关的流体动力变量(密度、温度和速度),使用尼克斯模拟数据。我们显示,我们的方法能够以20kpc美元的分辨率快速估算这些领域,并以远比现有近似值更精确得多的方式捕捉Ly$(alpha)森林的统计数据。由于我们的模型是完全革命性的,我们可以训练较小的模拟箱,并部署大得多的模拟变量,从而节省大量计算费用。此外,由于我们的方法可以直接产生流体动力场的近似值,而不是利-阿尔法元的通量,我们的方法并不局限于对电离子背景的特定选择或中值传输通量。