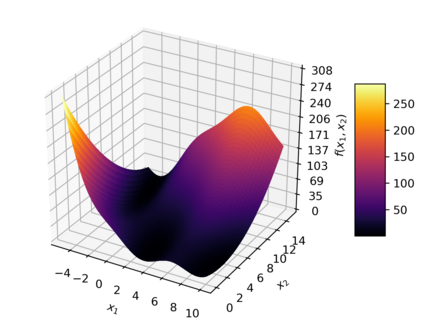
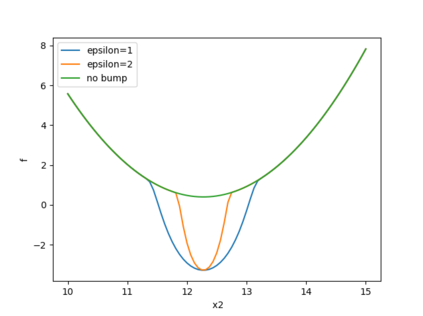
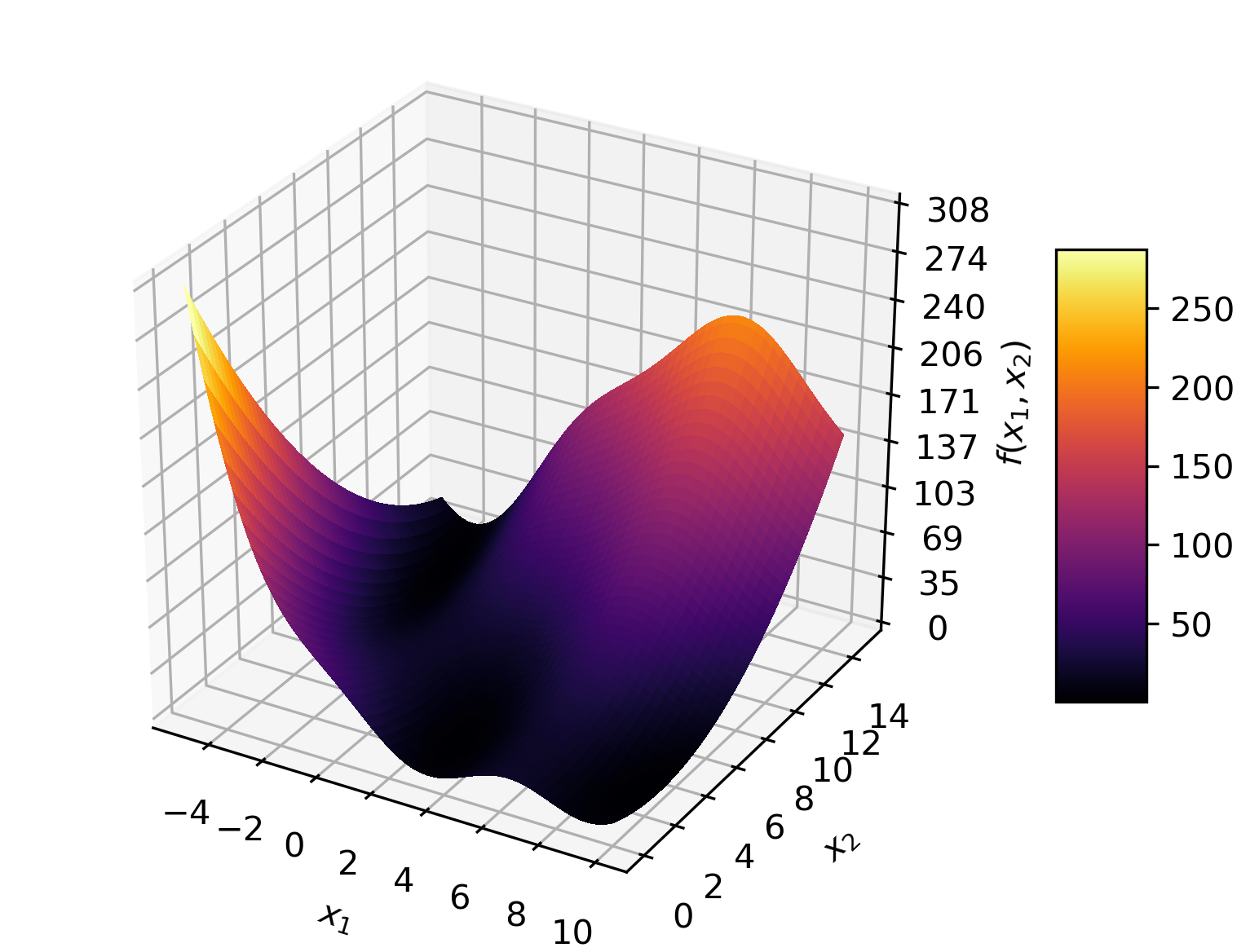
Some popular functions used to test global optimization algorithms have multiple local optima, all with the same value, making them all global optima. It is easy to make them more challenging by fortifying them via adding a localized bump at the location of one of the optima. In previous work the authors illustrated this for the Branin-Hoo function and the popular differential evolution algorithm, showing that the fortified Branin-Hoo required an order of magnitude more function evaluations. This paper examines the effect of fortifying the Branin-Hoo function on surrogate-based optimization, which usually proceeds by adaptive sampling. Two algorithms are considered. The EGO algorithm, which is based on a Gaussian process (GP) and an algorithm based on radial basis functions (RBF). EGO is found to be more frugal in terms of the number of required function evaluations required to identify the correct basin, but it is expensive to run on a desktop, limiting the number of times the runs could be repeated to establish sound statistics on the number of required function evaluations. The RBF algorithm was cheaper to run, providing more sound statistics on performance. A four-dimensional version of the Branin-Hoo function was introduced in order to assess the effect of dimensionality. It was found that the difference between the ordinary function and the fortified one was much more pronounced for the four-dimensional function compared to the two dimensional one.
翻译:用于测试全球优化算法的一些流行功能具有多重本地opima, 全部具有相同的价值, 使它们成为全球opima 。 很容易通过在 Opima 的某个位置添加本地拼图来强化它们来使其更具挑战性。 在以前的工作中, 作者为Branin- Hoo 函数和流行化差异演算法展示了这一点, 表明强化的Branin- Hooo 功能需要数量级级的更多功能评估。 本文审查了将Branin- Hoo 函数强化为基于代理功能优化( 通常通过适应性取样进行) 的效果。 考虑了两种算法。 EGO 算法基于一个 Gaussian 进程( GP) 和一个基于辐射功能的算法( RBFF ) 。 在确定正确基础所需的职能评估数量方面, EGOGO更加节节节节节节, 但是在台式上运行费用昂贵, 可以重复多少次运行, 以建立关于所需功能评估次数的正确统计。 RBFF 算法比较便宜, 运行更方便,, 提供更准确的功能的运行, 提供更可靠的关于正常性的一般功能的一维度的统计。 的四维次元的四维函数之间, 被找到的四维 。 。