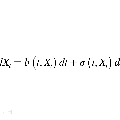Although statistical inference in stochastic differential equations (SDEs) driven by Wiener process has received significant attention in the literature, inference in those driven by fractional Brownian motion seem to have seen much less development in comparison, despite their importance in modeling long range dependence. In this article, we consider both classical and Bayesian inference in such fractional Brownian motion based SDEs. In particular, we consider asymptotic inference for two parameters in this regard; a multiplicative parameter associated with the drift function, and the so-called "Hurst parameter" of the fractional Brownian motion, when the time domain tends to infinity. For unknown Hurst parameter, the likelihood does not lend itself amenable to the popular Girsanov form, rendering usual asymptotic development difficult. As such, we develop increasing domain infill asymptotic theory, by discretizing the SDE. In this setup, we establish consistency and asymptotic normality of the maximum likelihood estimators, as well as consistency and asymptotic normality of the Bayesian posterior distributions. However, classical or Bayesian asymptotic normality with respect to the Hurst parameter could not be established. We supplement our theoretical investigations with simulation studies in a non-asymptotic setup, prescribing suitable methodologies for classical and Bayesian analyses of SDEs driven by fractional Brownian motion. Applications to a real, close price data, along with comparison with standard SDE driven by Wiener process, is also considered. As expected, it turned out that our Bayesian fractional SDE triumphed over the other model and methods, in both simulated and real data applications.
翻译:尽管已经在维纳过程驱动的随机微分方程中获得了显着的统计推断成果,在分数布朗运动驱动的随机微分方程中进行推断似乎相对较少,尽管这种模型在长程依存建模中非常重要。本文中,我们考虑这种基于分数布朗运动的随机微分方程的经典和贝叶斯推断。特别地,我们考虑两个参数的渐进推断,一个与漂移函数有关的乘法参数,另一个是分数布朗运动的 "Hurst参数",当时间域趋近于无限大时。对于未知的Hurst参数,似然函数不容易适用于流行的Girsanov形式,使得通常的渐进发展困难。因此,我们通过离散化SDE,发展域内填充渐进理论。在这个设置中,我们确立了最大似然估计的一致性和渐进正态性,以及贝叶斯后验分布的一致性和渐进正态性。然而,无法建立一个关于Hurst参数的经典或贝叶斯渐进正态性。我们通过模拟研究的非渐进设置来补充我们的理论研究,并规定适当的经典和贝叶斯分析分数布朗运动驱动的SDE的方法。我们还讨论了内含真实交易价格数据的应用,同时考虑了与标准维纳驱动的SDE的比较。预期的是,在模拟和实际数据应用中,我们的贝叶斯分数SDE优于其他模型和方法。