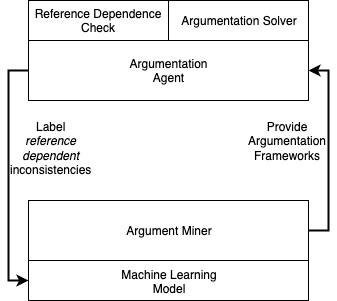
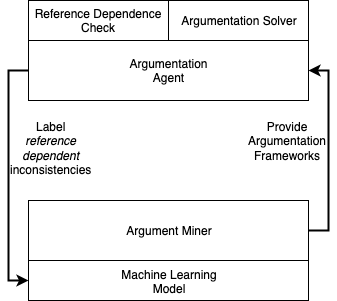
Abstract argumentation has emerged as a method for non-monotonic reasoning that has gained popularity in the symbolic artificial intelligence community. In the literature, the different approaches to abstract argumentation that were refined over the years are typically evaluated from a formal logics perspective; an analysis that is based on models of economically rational decision-making does not exist. In this paper, we work towards addressing this issue by analyzing abstract argumentation from the perspective of the rational man paradigm in microeconomic theory. To assess under which conditions abstract argumentation-based decision-making can be considered economically rational, we derive reference independence as a non-monotonic inference property from a formal model of economic rationality and create a new argumentation principle that ensures compliance with this property. We then compare the reference independence principle with other reasoning principles, in particular with cautious monotony and rational monotony. We show that the argumentation semantics as proposed in Dung's seminal paper, as well as other semantics we evaluate -- with the exception of naive semantics and the SCC-recursive CF2 semantics -- violate the reference independence principle. Consequently, we investigate how structural properties of argumentation frameworks impact the reference independence principle, and identify cyclic expansions (both even and odd cycles) as the root of the problem. Finally, we put reference independence into the context of preference-based argumentation and show that for this argumentation variant, which explicitly models preferences, reference independence cannot be ensured in a straight-forward manner.
翻译:在文献中,多年来完善的抽象论理的不同理论方法通常从正式逻辑角度加以评估;根据经济合理决策模式进行的分析并不存在。在本文件中,我们致力于通过从微观经济理论中理性人范的角度分析抽象论理来解决这一问题。为了评估抽象论理决策在哪些条件下可以被视为经济合理,我们从正式的经济合理性模型中将独立作为非口头推论属性,并创建新的论证原则,以确保该财产得到遵守。我们随后将参考独立原则与其他推理原则进行比较,特别是谨慎的单调和理性单调原则。我们表明,从微观经济理论中理性人范的角度分析抽象论理,以及我们所评价的其他语义学学学,除了天真的语义学和SCC-CF2选义外,我们从正式的经济合理性模型中将独立作为非口头推论性推理属性,从而违反参考独立原则。因此,我们最终将参考独立原则与其他推理学原则进行比较,从结构学角度来说明独立性问题。我们从结构学的角度来研究,将这种推理学上的独立性问题,我们把这种推理学论作为推理论的推理作为推理的推理性推论的推理,我们最后将之推理性推理,将解释性推论作为推论的推论的推论作为推理,将之推理,我们将之的推理法性推理法论是解释性推论的推论的推论的推论是,我们推理,将解释性推理,将之推论的推论的推论的推论的推论的推论的推论的推论的推论是,我们推理性推理性推论是分性推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推理,将之推论是推论的推论,最后,将之推论是,将之推论,将之推论是,最后我们推论是,将之推论是,将之推论是推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推论的推论是,我们推论理,最后我们推论的推理,